
【题目】已知F是抛物线![]() 的焦点,点M是抛物线上的定点,且
的焦点,点M是抛物线上的定点,且![]() .
.
(1)求抛物线C的方程;
(2)直线AB与抛物线C交于不同两点![]() ,直线
,直线![]() 与AB平行,且与抛物线C相切,切点为N,试问△ABN的面积是否是定值.若是,求出这个定值;若不是,请说明理由.
与AB平行,且与抛物线C相切,切点为N,试问△ABN的面积是否是定值.若是,求出这个定值;若不是,请说明理由.
【答案】(1)![]() ;(2)定值
;(2)定值![]()
【解析】
(1)设![]() ,由
,由![]() ,求得
,求得![]() ,代入抛物线的方程,求得
,代入抛物线的方程,求得![]() 的值,即可得到抛物线的方程;
的值,即可得到抛物线的方程;
(2)设其方程为![]() ,联立方程组,求得
,联立方程组,求得![]() ,得到Q
,得到Q![]() ,
,
由条件设切线的方程为![]() ,联立方程组,利用根与系数的关系,求得切点N
,联立方程组,利用根与系数的关系,求得切点N![]() ,再由
,再由![]() 轴,求得
轴,求得![]() 及
及![]() ,利用面积公式,即可求解。
,利用面积公式,即可求解。
(1)设![]() ,由题知
,由题知![]() ,所以
,所以![]() ,
,
所以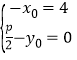 ,即
,即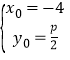 ,
,
代入![]() 中得
中得![]() ,解得
,解得![]() ,
,
所以抛物线C的方程为![]() 。
。
(2)由题意知,直线AB的斜率存在,设其方程为![]() ,
,
由![]() ,整理得
,整理得![]() ,则
,则![]() ,
,
所以![]() ,
,
设AB的中点为Q,则点Q的坐标为![]() ,
,
由条件设切线的方程为![]() ,则
,则![]() ,整理得
,整理得![]() 。
。
因为直线与抛物线相切,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以切点N的坐标为![]() ,
,
所以![]() 轴,所以
轴,所以![]() ,
,
因为![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的面积为定值,且定值为
的面积为定值,且定值为![]()


科目:高中数学 来源: 题型:
【题目】如图,某人工景观湖外围有两条相互垂直的直线型公路ll,l2,且ll和l2交于点O.为了方便游客游览,计划修建一条连接公路与景观湖的直线型公路AB.景观湖的轮廓可以近似看成一个圆心为O,半径为2百米的圆,且公路AB与圆O相切,圆心O到ll,l2的距离均为5百米,设OAB=![]() ,AB长为L百米.
,AB长为L百米.
(1)求L关于![]() 的函数解析式;
的函数解析式;
(2)当![]() 为何值时,公路AB的长度最短?
为何值时,公路AB的长度最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在![]() 上的单调函数,且对任意的x∈
上的单调函数,且对任意的x∈![]() 都有
都有![]() ,则方程
,则方程![]() 的一个根所在的区间是( )
的一个根所在的区间是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x2+mx+1=0有两个不等的负根;命题q:4x2+4(m﹣2)x+1=0无实根.若命题p与命题q有且只有一个为真,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生从全校学生中随机选取![]() 名统计他们的鞋码大小,得到如下数据:
名统计他们的鞋码大小,得到如下数据:
鞋码 |
|
|
|
|
|
|
|
|
|
| 合计 |
男生 |
|
|
|
|
|
|
|
|
| ||
女生 |
|
|
|
|
|
|
|
|
|
以各性别各鞋码出现的频率为概率.
(![]() )从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率.
)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率.
(![]() )为了解该校学生考试作弊的情况,从该校随机挑选
)为了解该校学生考试作弊的情况,从该校随机挑选![]() 名学生进行抽样调查.每位学生从装有除颜色外无差别的
名学生进行抽样调查.每位学生从装有除颜色外无差别的![]() 个红球和
个红球和![]() 个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到
个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到![]() 张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com