
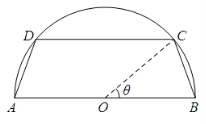
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形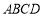 (如图所示,其中O为圆心,
(如图所示,其中O为圆心, 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求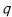 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
(1)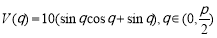 ;(2)
;(2)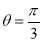 ;(3)是.
;(3)是.
【解析】
试题分析:(1)本题求直四棱柱的体积,关键是求底面面积,我们要用底面半径1和 表示出等腰梯形的上底
表示出等腰梯形的上底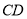 和高,从图形中可知高为
和高,从图形中可知高为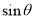 ,而
,而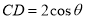 ,因此面积易求,体积也可得出;(2)我们在(1)中求出
,因此面积易求,体积也可得出;(2)我们在(1)中求出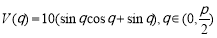 ,这里
,这里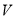 的最大值可利用导数知识求解,求出
的最大值可利用导数知识求解,求出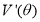 ,解出方程
,解出方程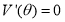 在
在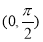 上的解,然后考察在解
上的解,然后考察在解 的两边
的两边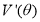 的正负性,确定
的正负性,确定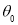 是最大值点,实质上对应用题来讲,导数值为0的那个唯一点就是要求的极值点);(3),上(2)我们可能把木梁的表面积用
是最大值点,实质上对应用题来讲,导数值为0的那个唯一点就是要求的极值点);(3),上(2)我们可能把木梁的表面积用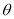 表示出来,
表示出来,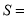
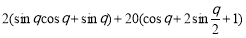
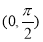 ,由于
,由于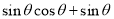 在体积
在体积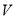 中出现,因此我们可求
中出现,因此我们可求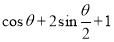 的最大值,这里可不用导数来求,因为
的最大值,这里可不用导数来求,因为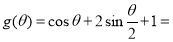
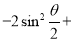
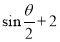 ,可借助二次函数知识求得最大值,如果这里
,可借助二次函数知识求得最大值,如果这里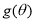 取最大值时的
取最大值时的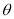 和
和 取最大值的
取最大值的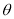 取值相同,则结论就是肯定的.
取值相同,则结论就是肯定的.
试题解析:(1)梯形 的面积
的面积
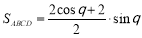 =
=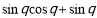 ,
,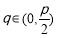 . 2分
. 2分
体积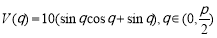 . 3分
. 3分
(2)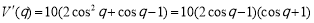 .
.
令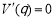 ,得
,得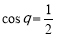 ,或
,或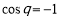 (舍).
(舍).
∵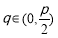 ,∴
,∴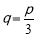 . 5分
. 5分
当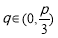 时,
时,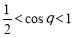 ,
,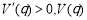 为增函数;
为增函数;
当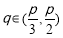 时,
时,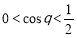 ,
,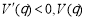 为减函数. 7分
为减函数. 7分
∴当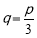 时,体积V最大. 8分
时,体积V最大. 8分
(3)木梁的侧面积 =
=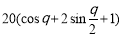 ,
,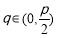 .
.
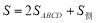 =
=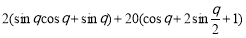 ,
,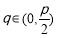 . 10分
. 10分
设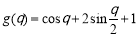 ,
,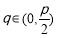 .∵
.∵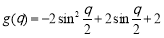 ,
,
∴当 ,即
,即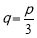 时,
时,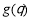 最大. 12分
最大. 12分
又由(2)知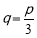 时,
时,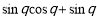 取得最大值,
取得最大值,
所以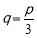 时,木梁的表面积S最大. 13分
时,木梁的表面积S最大. 13分
综上,当木梁的体积V最大时,其表面积S也最大. 14分
考点:(1)函数解析式;(2)用导数求最值;(3)四棱柱的表面积及其最值.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知数列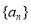 的前
的前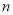 项和为
项和为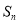 ,对一切正整数
,对一切正整数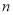 ,点
,点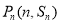 都在函数
都在函数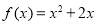 的图像上,且过点
的图像上,且过点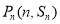 的切线的斜率为
的切线的斜率为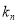 .
.
(1)求数列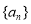 的通项公式;
的通项公式;
(2)设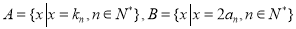 ,等差数列
,等差数列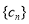 的任一项
的任一项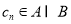 ,其中
,其中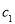 是
是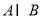 中所有元素的最小数,
中所有元素的最小数,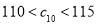 ,求
,求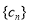 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三百校联合调研测试(一)数学试卷(解析版) 题型:解答题
如图,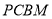 是直角梯形,∠
是直角梯形,∠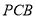 =90°,
=90°,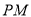 ∥
∥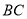 ,
,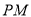 =1,
=1,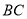 =2,又
=2,又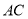 =1,∠
=1,∠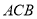 =120°,
=120°,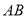 ⊥
⊥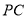 ,直线
,直线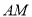 与直线
与直线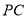 所成的角为60°.
所成的角为60°.
(1)求二面角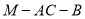 的的余弦值;
的的余弦值;
(2)求点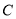 到面
到面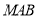 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三百校联合调研测试(一)数学试卷(解析版) 题型:填空题
一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出 人.
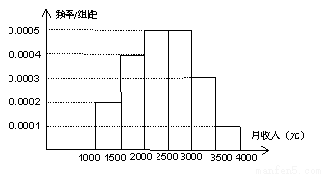
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:填空题
如图,在△ABC中,BO为边AC上的中线,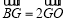 ,设
,设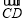 ∥
∥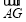 ,若
,若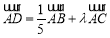
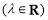 ,则
,则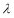 的值为 .
的值为 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试文科数学试卷(解析版) 题型:填空题
从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:填空题
四棱锥P ? ABCD 的底面ABCD是边长为2的正方形,PA⊥底面ABCD且PA=4,则PC与底面ABCD所成角的正切值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com