
分析 写出原命题的逆命题,可判断①;根据充要条件的定义,可判断②;写出原命题的否定,可判断③;判断函数的零点个数,可判断④.
解答 解:命题“若x=$\frac{π}{6}$,则sinx=$\frac{1}{2}$”的逆命题为“若sinx=$\frac{1}{2}$,则x=$\frac{π}{6}$”,为假命题,故①错误;
设a,b是实数,则a<b时,a2<b2不一定成立,a2<b2时,a<b不一定成立,
故a<b是a2<b2的既不充分而不必要条件,故②错误;
命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,都有x2+x+1≥0”,故③错误;
函数f(x)=lnx+x-$\frac{3}{2}$在区间(1,2)上单调递增,且f(1)•f(2)=$-\frac{1}{2}$•(ln2+$\frac{1}{2}$)<0,故函数f(x)=lnx+x-$\frac{3}{2}$在区间(1,2)上有且仅有一个零点,故④正确;
故错误的结论有:①②③,
故答案为:①②③
点评 本题以命题的真假判断为载体,考查了四种命题,充要条件,存在性命题的否定,零点存在定理,难度中档.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
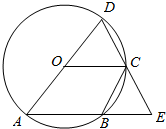 如图,AD是⊙O的直径,B为⊙O上的一点,连接AB并延长至点E,使得AE=AD,连接DE,交⊙O于点C,连接OC.
如图,AD是⊙O的直径,B为⊙O上的一点,连接AB并延长至点E,使得AE=AD,连接DE,交⊙O于点C,连接OC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 0 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0” | |
| B. | 若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 | |
| C. | △ABC中,sinA>sinB是A>B的充要条件 | |
| D. | 若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$>0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com