
函数f(x)=loga|x-1|在(0,1)上递减,那么f(x)在区间(1,+∞)上,下列说法正确的是
A.递增且无最大值
B.递减且无最小值
C.递增且有最大值
D.递减且有最小值
|
解:因为x∈(0,1)时,|x-1|<1且t=|x-1|为减函数,又函数f(x)=loga|x-1|在(0,1)上递减,所以函数y=logat为增函数,故a>1. 又因为t=|x-1|在区间(1,+∞)上为增函数,所以f(x)=loga|x-1|在区间(1,+∞)上为增函数,且无最大值,故选A. 点评:本题利用图象可能会好理解,将函数y=loga|x|的图象向右平移1个单位得到函数f(x)=loga|x-1|的图象,又在(0,1)上递减,所以可以得到a>1.然后可以直接根据图象判定答案为递增且无最大值. |
|
本题是复合函数单调性的问题,可以利用复合函数单调性的规律作出判断,但也可直接通过图象,利用数形结合帮助理解. |


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修1) 2009-2010学年 第8期 总164期 人教课标高一版 题型:013
函数f(x)=log![]() (x2-2x+5)的值域是
(x2-2x+5)的值域是
[-2,+∞)
(-∞,-2]
(0,1)
(-∞,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=log![]() (3x2-ax+5)在[-1,+∞)上是减函数,则实数a的取值范围是( )
(3x2-ax+5)在[-1,+∞)上是减函数,则实数a的取值范围是( )
A.-8≤a≤-6 B.-8<a<-6
C.-8<a≤-6 D.a≤-6
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四1.4三角函数的图像与性质练习卷(三)(解析版) 题型:解答题
已知函数f(x)=log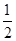 |sinx|.
|sinx|.
(1)求其定义域和值域;
(2)判断其奇偶性;
(3)求其周期;
(4)写出单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com