Question

在正方体ABCD—A₁B₁C₁D₁中，E、F分别为棱BB₁和DD₁的中点.

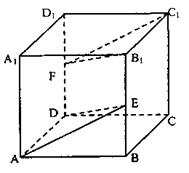
（1）求证：平面B₁FC//平面ADE；

（2）试在棱DC上取一点M，使平面ADE；

（3）设正方体的棱长为1，求四面体A­₁—FEA的体积.

 

Answer 1

【答案】

（1）E、F分别为正方体ABCD—A₁B₁C₁D₁棱BB₁和DD₁中点. 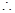四边形DFB₁E为平行四边形，即FB₁//DE，由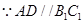又

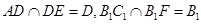
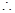平面B₁FC//平面ADE（2）取DC中点M（3）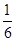

【解析】

试题分析：（1）证明：E、F分别为正方体ABCD—A₁B₁C₁D₁棱BB₁和DD₁中点.

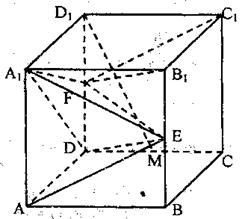
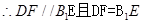
四边形DFB₁E为平行四边形，

即FB₁//DE，

由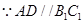       2分

又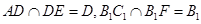

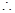平面B₁FC//平面ADE.       4分

（2）证明：取DC中点M，连接D₁M，

由正方体性质可知，，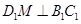

且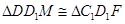        5分

所以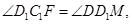

又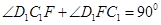

所以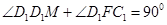

所以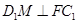       6分

又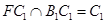

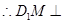平面B₁FC₁

又由（1）知平面B₁FC₁//平面ADE.

所以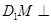平面ADE.       8分

（3）方法一：由正方体性质有点F到棱AA₁的距离及点E到侧面A₁ADD₁的距离都是棱长1  9分

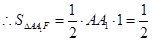
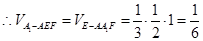     12分

方法二：取EF中点O₁，

把四面体分割成两部分F—AA₁O₁，E—AA₁O₁

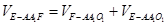        10分

E、F分 为正方体ABCD—A₁B₁C₁D₁棱BB₁和DD₁中点，

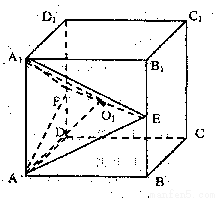
由正方体性质有，O₁为正方体的中心.

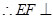平面AA₁O，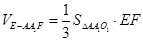

O₁到AA₁的距离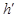为面对角线的一半，

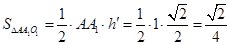
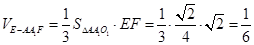      12分

考点：线面垂直平行的判定与椎体体积

点评：判定两面平行常用的方法是其中一个平面内两条相交直线平行于另外一面；判定线面垂直常用方法是直线垂直于平面内两条相交直线；椎体体积