练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．复数z=$\frac{a-i}{1+i}$（a∈R，i是虚数单位）在复平面上对应的点不可能位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    分析 利用复数代数形式的乘除运算化简，由实部和虚部不同时大于0说明z在复平面上对应的点不可能位于第一象限．

    解答 解：∵$z=\frac{a-i}{1+i}$=$\frac{（a-i）（1-i）}{（1+i）（1-i）}=\frac{a-1-（a+1）i}{2}=\frac{a-1}{2}-\frac{a+1}{2}i$，
    ∴z在复平面上对应的点的坐标为（$\frac{a-1}{2}，-\frac{a+1}{2}$），
    若a-1＞0，则a＞1，∴a+1＜0．
    ∴z在复平面上对应的点不可能位于第一象限．
    故选：A．

    点评 本题考查复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．在△ABC中，若a2=b2+c2-$\sqrt{3}$bc，则角A的度数为（　　）
    A．30°B．150°C．60°D．120°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

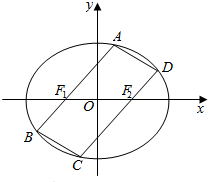    15．已知椭圆E的中心在坐标原点，左、右焦点F1、F2分别在x轴上，离心率为$\frac{1}{2}$，在其上有一动点A，A到点F1距离的最小值是1，过A、F1作一个平行四边形，顶点A、B、C、D都在椭圆E上，如图所示．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）判断?ABCD能否为菱形，并说明理由．
    （Ⅲ）当?ABCD的面积取到最大值时，判断?ABCD的形状，并求出其最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知$cos（\frac{π}{2}-α）=\frac{3}{5}，α∈（{\frac{π}{2}，π}）$，则$sin（{α+\frac{π}{3}}）$=$\frac{{3-4\sqrt{3}}}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知3i-2是关于x的方程2x2+px+q=0的一个根，则实数p+q=34．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若幂函数f（x）的图象过点$（{\;2\;，\;\frac{{\sqrt{2}}}{2}\;}）$，则f-1（2）=$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．一个几何体的三视图如图所示，则这个几何体的体积等于（　　）
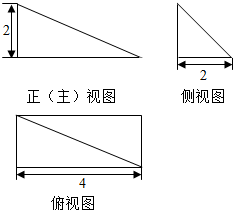
    A．12B．4C．$\frac{16}{3}$D．$\frac{8\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F（-1，0），点F到右顶点的距离为$\sqrt{2}$+1．
    （1）求该椭圆方程；
    （2）已知经过点F且垂直于x轴的直线交椭圆于A，B两点，点M（-$\frac{5}{4}$，0），求$\overrightarrow{MA}$•$\overrightarrow{MB}$的值；
    （3）若经过点F的动直线l与椭圆交于不同的两点A，B，点M（-$\frac{5}{4}$，0），问$\overrightarrow{MA}$•$\overrightarrow{MB}$是否为定值？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．函数y=2sin（2x+$\frac{π}{3}$）的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（　　）
    A．$\frac{π}{12}$B．$\frac{π}{6}$C．$\frac{π}{3}$D．$\frac{5π}{6}$

    查看答案和解析>>

    同步练习册答案