
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
⑴ 求![]() ,
, ![]() 的值;
的值;
⑵ 直接写出![]() 时,
时, ![]() 的取值范围。
的取值范围。

【答案】(1)k2=2或k1=-1;(2)![]() 。
。
【解析】试题分析:(1)先证明△DOA≌△AEB 及△DOA≌ △CFD ,进而推得BE=OA=DF=m AE=OD=CF=2-m ,从而说明两点C(2-m,2),B(2,m)都在双曲线上,然后建立方程求出m的值;(2)借助两点C(1,2),B(2,1)的坐标结合题设所提供的图像可写出不等式![]() 的解集。
的解集。
解:(1) 解:过点B作BE⊥x轴于E,
过点C作CF⊥y轴于F.
∵四边形ABCD是正方形
∴∠BAD=90° AB=AD
∵∠OAE=180°
∴∠1+∠2=90°
又x轴⊥y轴
∴∠2+∠3=90°
∴∠1 =∠3
∴△DOA≌△AEB
同理△DOA≌ △CFD
∴BE=OA=DF=m AE=OD=CF=2-m
∴点C(2-m,2)
又点C(2-m,2),B(2,m)在双曲线上
∴2(2-m)=2m m =1
∴ B(2,1) C(1,2)
∴k2=2 k1=-1
⑵![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 和
和![]() 公共弦的长度.
公共弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各2张,让孩子从盒子里任取3张卡片,按卡片上最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量x的分布列;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图①,正三角形![]() 的边长为4,
的边长为4,![]() 是
是![]() 边上的高,
边上的高,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 边的中点,现将△
边的中点,现将△![]() 沿
沿![]() 翻折成直二面角
翻折成直二面角![]() ,如图②.
,如图②.
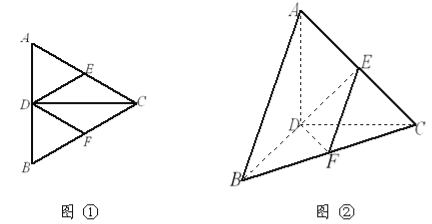
(1)判断直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附: 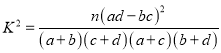 ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)甲、乙两袋中各装有大小相同的小球![]() 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为![]() 、
、![]() 、
、![]() ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为![]() ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com