
【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以![]() (个)(其中
(个)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利润.
(元)表示利润.
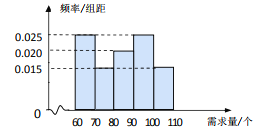
(1)根据直方图计算需求量的中位数;
(2)估计利润![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的数学期望.
的数学期望.
【答案】(1)85个;(2) ![]() ;(3)142.
;(3)142.
【解析】试题分析:(1)需求量的中位数![]() (个)
(个)
(2)由题意可得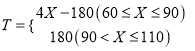 .
.
设利润![]() 不少于100元为事件
不少于100元为事件![]() ,利润
,利润![]() 不少于100元时, 可得
不少于100元时, 可得![]() ,即
,即![]() ,由直方图可知,由此可估计当
,由直方图可知,由此可估计当![]() 时的概率.
时的概率.
(3)由题意,可得利润![]() 的取值可为:80,120,160,180,分别求得
的取值可为:80,120,160,180,分别求得
![]() ,得到利润
,得到利润![]() 的分布列,则
的分布列,则![]() 的数学期望可求.
的数学期望可求.
试题解析:(1)需求量的中位数![]() (个)(其它解法也给分)
(个)(其它解法也给分)
(2)由题意,当![]() 时,利润
时,利润![]() ,
,
当![]() 时,利润
时,利润![]() ,
,
即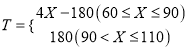 .
.
设利润![]() 不少于100元为事件
不少于100元为事件![]() ,利润
,利润![]() 不少于100元时,即
不少于100元时,即![]() ,
,
∴![]() ,即
,即![]() ,由直方图可知,当
,由直方图可知,当![]() 时,
时,
所求概率: ![]()
(3)由题意,由于![]() ,
,
故利润![]() 的取值可为:80,120,160,180,
的取值可为:80,120,160,180,
且![]() ,
,
故得分布列为:
![]()
利润的数学期望![]() .
.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin (2x+ ![]() ).
).
(1)求函数f(x)的最小正周期及其单调减区间;
(2)用“五点法”画出函数g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人,若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(1)求表格中的数据![]() ;
;
(2)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.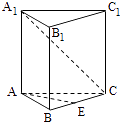
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,其离心率为
,其离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相交于
相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为正三角形,若存在,求直线
为正三角形,若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是 . (填写所有正确的序号) ①若sinx+siny= ![]() ,则siny﹣cos2x的最大值为
,则siny﹣cos2x的最大值为 ![]() ;
;
②函数y=sin(2x+ ![]() )的单调增区间是[kπ﹣
)的单调增区间是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
③函数f(x)= ![]() 是奇函数;
是奇函数;
④函数y=tan ![]() ﹣
﹣ ![]() 的最小正周期是π.
的最小正周期是π.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com