
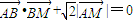 ,点M的轨迹K.若过点B的直线L1(斜率不等于0)与轨迹K交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
,点M的轨迹K.若过点B的直线L1(斜率不等于0)与轨迹K交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.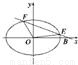 (1)由x2=4y得y=
(1)由x2=4y得y= x2,用导数法求得直线l的斜率,再求得其方程,令y=0得点A坐标;
x2,用导数法求得直线l的斜率,再求得其方程,令y=0得点A坐标;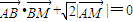 =0得得
=0得得 +y2=1.知轨迹K是椭圆,设
+y2=1.知轨迹K是椭圆,设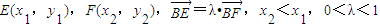
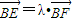 ,即为两个三角形面积之比,只要求得λ即可.
,即为两个三角形面积之比,只要求得λ即可.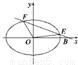 解:(1)由x2=4y得y=
解:(1)由x2=4y得y= x2,y′=
x2,y′= x.
x.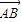 =(1,0),
=(1,0),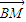 =(x-2,y),
=(x-2,y),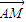 =(x-1,y),
=(x-1,y),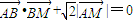 =0得(x-2)+y•0+
=0得(x-2)+y•0+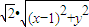 =0,
=0,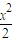 +y2=1.轨迹K是椭圆.(9分)
+y2=1.轨迹K是椭圆.(9分)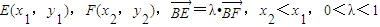
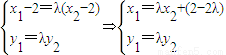
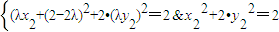
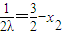 ①(11分)
①(11分)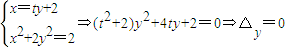
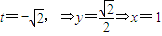 得切点(1,
得切点(1,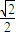 )
)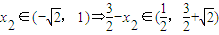
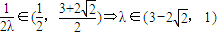
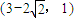 .(15分)
.(15分)

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
| x2 |
| 2 |
| y2 |
| a |
| OR |
| OS |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| BM |
| 2 |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
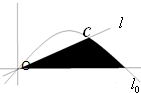 已知直线l与抛物线C,当直线l从l0开始在平面上绕O点按逆时针方向匀速旋转(旋转的角度不超过90°)时,它扫过的面积S是时间t的函数,则函数图象大致是( )
已知直线l与抛物线C,当直线l从l0开始在平面上绕O点按逆时针方向匀速旋转(旋转的角度不超过90°)时,它扫过的面积S是时间t的函数,则函数图象大致是( )查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 20 |
| 1 |
| 4 |
| 1 |
| 25 |
| x2 |
| 2 |
| y2 |
| a |
| OR |
| OS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com