
【题目】(1)求![]() 的展开式中
的展开式中![]() 的系数及展开式中各项系数之和;
的系数及展开式中各项系数之和;
(2)从0,2,3,4,5,6这6个数字中任取4个组成一个无重复数字的四位数,求满足条件的四位数的个数.
【答案】(1)![]() (2)300
(2)300
【解析】试题分析:(1)直接利用二项展开式定理求解即可展开式中![]() 的系数,令
的系数,令![]() 即可得结果;(2)分选
即可得结果;(2)分选![]() ,不选
,不选![]() 两种情况讨论,再利用分类计数加法原理可得结果.
两种情况讨论,再利用分类计数加法原理可得结果.
试题解析:(1)∵![]() ,∴展开式中
,∴展开式中![]() 的系数为
的系数为![]() .
.
令![]() ,得各项系数之和为
,得各项系数之和为![]() .
.
(2)若不选0,则有![]() 个;
个;
若选0,则有![]() 个.
个.
故能组成![]() 个不同的四位数.
个不同的四位数.
【方法点晴】本题主要考查二项展开式定理的通项与系数及排列组合综合问题,属于中档题题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式![]() ;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.
;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 经过点A (1,0).
经过点A (1,0).
(1)若直线![]() 与圆C相切,求直线
与圆C相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
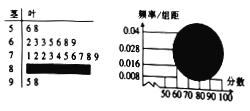
【题目】如图,某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分,据此解答如下问题:
(1)求该班全体男生的人数及分数在![]() 之间的男生人数;
之间的男生人数;
(2)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表);
(3)从分数在![]() 中抽取两个男生,求抽取的两男生分别来自
中抽取两个男生,求抽取的两男生分别来自![]() 、
、![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经测算,某型号汽车在匀速行驶过程中每小时耗油量![]() (升)与速度
(升)与速度![]() (千米/每小时)
(千米/每小时) ![]() 的关系可近似表示为:
的关系可近似表示为: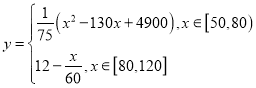 .
.
(Ⅰ)该型号汽车速度为多少时,可使得每小时耗油量最低?
(Ⅱ)已知![]() 两地相距120公里,假定该型号汽车匀速从
两地相距120公里,假定该型号汽车匀速从![]() 地驶向
地驶向![]() 地,则汽车速度为多少时总耗油量最少?
地,则汽车速度为多少时总耗油量最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
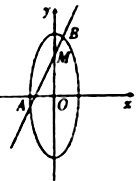
【题目】如图,已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为
,离心率为![]() ,以椭圆
,以椭圆![]() 的端州的两端点和两焦点所围成的四边形的周长为8,直线
的端州的两端点和两焦点所围成的四边形的周长为8,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)若函数![]() 在
在![]() 处取到最小值
处取到最小值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),再将向左平移
倍(纵坐标不变),再将向左平移![]() 个单位,得到的函数图象关于
个单位,得到的函数图象关于![]() 轴对称,求函数
轴对称,求函数![]() 的单调递增区间。
的单调递增区间。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表
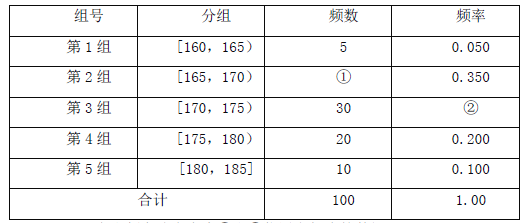
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5 组中用分层抽样的方法抽取6 名学生进行体能测试,求第3,4,5 组每组各应抽取多少名学生进行测试;
(Ⅲ)在(Ⅱ)的前提下,学校决定在6 名学生中随机抽取2 名学生进行引体向上测试,求第4 组中至少有一名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com