考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(I)连接AC交BD于点O,连接EO.由三角形的中位线定理可得AC1∥EO.再利用线面平行的判定定理即可得出.
((III)连接BA1,A1C1.可得△A1BC1为等边三角形,四边形A1BCD1为平行四边形.于是A1B∥CD1,∠A1BC1为异面直线BC1,CD1所成角.
解答:
(I)证明:连接AC交BD于点O,连接EO.
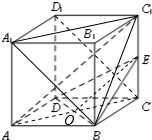
则AO=OC,又E是棱CC
1的中点.
∴AC
1∥EO.
∵EO?平面BDE,AC
1?平面BDE,
∴AC
1∥平面BDE;
(II)V
三棱锥E-BCD=
S△BCD•EC=
××22×1=1.
(III)连接BA
1,A
1C
1.
则△A
1BC
1为等边三角形,四边形A
1BCD
1为平行四边形.
∴A
1B∥CD
1,
∴∠A
1BC
1为异面直线BC
1,CD
1所成角.
∴∠A
1BC
1=60°为异面直线BC
1,CD
1所成角.
点评:本题考查了正方体的性质、线面平行的判定定理、三角形的中位线定理、等边三角形的判定与性质、平行四边形的判定与性质定理、三棱锥的体积计算公式、异面直线所成的角,考查了推理能力与计算能力,属于中档题.

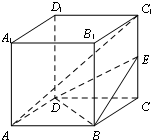 如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.

