
【题目】某植物园准备建一个五边形区域的盆栽馆,三角形ABE为盆裁展示区,沿AB、AE修建观赏长廊,四边形BCDE是盆栽养护区,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
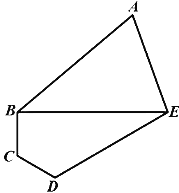
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求观赏长廊总长度AB+AE的取值范围。
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)六个从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有几种?
(2)把5件不同产品摆成一排,若产品![]() 与产品
与产品![]() 相邻,且产品
相邻,且产品![]() 与产品
与产品![]() 不相邻,则不同的摆法有几种?
不相邻,则不同的摆法有几种?
(3)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法有几种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱BCF﹣ADE的侧面CFED与ABFE都是边长为1的正方形,M、N两点分别在AF和CE上,且AM=EN.
(1)求证:平面ABCD⊥平面ADE;
(2)求证:MN∥平面BCF;
(3)若点N为EC的中点,点P为EF上的动点,试求PA+PN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com