
 和图象交于点Q,P、M分别是直线y=x与函数
和图象交于点Q,P、M分别是直线y=x与函数 的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .
的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 . 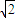 ,
,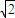 ),设M(a,
),设M(a, ),且 a>0,a≠
),且 a>0,a≠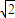 ,设P(b,b),则由PM≥PQ恒成立,可得
,设P(b,b),则由PM≥PQ恒成立,可得 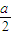 +
+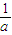 +
+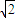 .由基本不等式可得
.由基本不等式可得 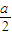 +
+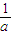 +
+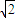 >2
>2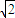 ,故 b≤2
,故 b≤2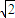 ,由此求得点P横坐标b的取值范围.
,由此求得点P横坐标b的取值范围.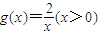 和图象交于点Q,∴点Q(
和图象交于点Q,∴点Q(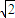 ,
,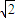 ).
).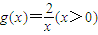 的图象上异于点Q的两点,
的图象上异于点Q的两点,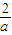 ),且 a>0,a≠
),且 a>0,a≠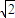 ,设P(b,b),则由PM≥PQ恒成立,
,设P(b,b),则由PM≥PQ恒成立,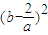 ≥
≥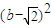 +
+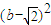 恒成立,化简可得 (2a+
恒成立,化简可得 (2a+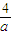 -4
-4 )b≤a2+
)b≤a2+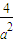 -4.
-4.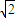 时,故(2a+
时,故(2a+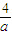 -4
-4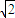 )>0,且 a2+
)>0,且 a2+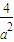 -4>0,由不等式可得
-4>0,由不等式可得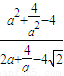 =
=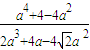 =
=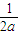 •
•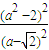 =
=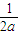 •
•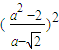
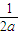 •
•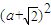 =
=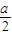 +
+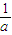 +
+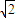 .
.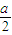 +
+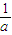 +
+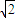 .
.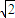 ,利用基本不等式可得
,利用基本不等式可得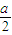 +
+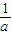 +
+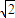 >2
>2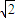 ,故 b≤2
,故 b≤2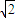 .
.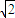 ,故点P横坐标b的取值范围是
,故点P横坐标b的取值范围是  ∪(
∪(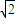 ,2
,2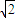 ].
].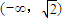 ∪(
∪( ,2
,2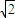 ].
].

科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| π |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| 2 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:江苏三模 题型:填空题
| 2 |
| x |
| 2 |
| x |
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏北四市高考数学三模试卷(解析版) 题型:填空题
 和图象交于点Q,P、M分别是直线y=x与函数
和图象交于点Q,P、M分别是直线y=x与函数 的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .
的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com