
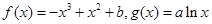 .
.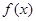 在
在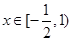 上的最大值为
上的最大值为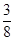 ,求实数
,求实数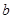 的值;
的值;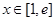 ,都有
,都有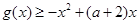 恒成立,求实数
恒成立,求实数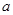 的取值范围;
的取值范围;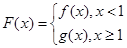 ,对任意给定的正实数
,对任意给定的正实数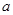 ,曲线
,曲线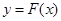 上是否存在两点
上是否存在两点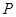 、
、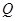 ,使得
,使得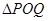 是以
是以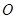 (
(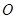 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在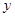 轴上?请说明理由。
轴上?请说明理由。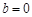 (2)
(2)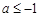 (3)对任意给定的正实数
(3)对任意给定的正实数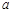 ,曲线
,曲线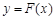 上总存在两点
上总存在两点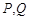 ,使得
,使得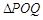 是以
是以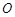 (
(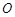 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在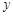 轴上
轴上 ,得
,得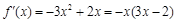 ,
,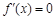 ,得
,得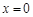 或
或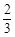 .
.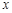 | 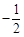 | 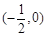 | 0 | 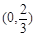 | 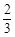 | 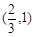 |
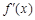 | | 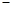 | 0 | 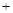 | 0 | 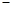 |
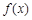 | 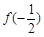 | 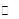 | 极小值 | 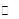 | 极大值 | 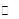 |
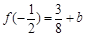 ,
,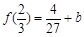 ,
,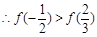 ,
,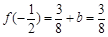 ,
,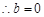 . 4分
. 4分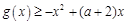 ,得
,得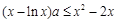 .
.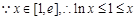 ,且等号不能同时取,
,且等号不能同时取,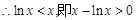 ,
,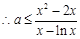 恒成立,即
恒成立,即 .
.  ,求导得,
,求导得,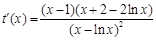 ,
,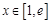 时,
时,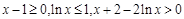 ,从而
,从而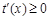 ,
,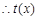 在
在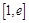 上为增函数,
上为增函数,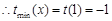 ,
,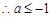 . 8分
. 8分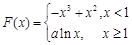 ,
,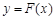 上存在两点
上存在两点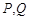 满足题意,则
满足题意,则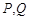 只能在
只能在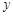 轴两侧,
轴两侧,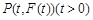 ,则
,则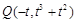 ,且
,且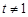 .
.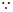
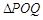 是以
是以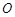 (
(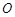 为坐标原点)为直角顶点的直角三角形,
为坐标原点)为直角顶点的直角三角形,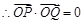 ,
,
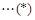 , 10分
, 10分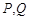 等价于方程
等价于方程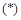 在
在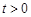 且
且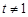 时是否有解.
时是否有解. 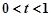 时,方程
时,方程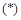 为
为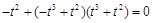 ,化简得
,化简得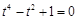 ,
,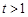 时,
时,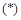 方程为
方程为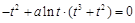 ,即
,即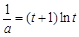 ,
,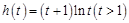 ,则
,则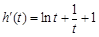 ,
,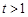 时,
时,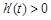 ,即
,即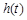 在
在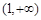 上为增函数,
上为增函数,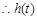 的值域为
的值域为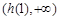 ,即
,即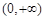 ,
,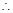 当
当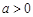 时,方程
时,方程 总有解.
总有解. 对任意给定的正实数
对任意给定的正实数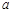 ,曲线
,曲线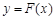 上总存在两点
上总存在两点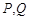 ,使得
,使得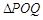 是以
是以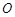 (
(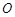 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在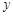 轴上. 14分
轴上. 14分 

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com