练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某广场上有4盏装饰灯，晚上每盏灯都随机地闪烁红灯或绿灯，每盏灯出现红灯的概率都是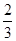，出现绿灯的概率都是.记这4盏灯中出现红灯的数量为X，当这排装饰灯闪烁一次时：
    (1)求X＝2时的概率；
    (2)求X的数学期望．

    (1)   (2)

    解析解：(1)依题意知：X＝2表示4盏装饰灯闪烁一次时，恰好有2盏灯出现红灯，而每盏灯出现红灯的概率都是，
    故X＝2时的概率P＝C4222＝.
    (2)法一　X的所有可能取值为0,1,2,3,4，依题意知
    P(X＝k)＝C4kk4－k(k＝0,1,2,3,4)．
    ∴X的概率分布列为

    X
    		0
    		1
    		2
    		3
    		4
    P





    ∴数学期望E(X)＝0×＋1×＋2×＋3×＋4×＝.
    法二　∵X服从二项分布，即X～B，
    ∴E(X)＝4×＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图，从A1(1，0，0)、A2(2，0，0)、B1(0，1，0)、B2(0，2，0)、C1(0，0，1)、C2(0，0，2)这6个点中随机选取3个点，将这3个点及原点O两两相连构成一个“立体”，记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内，此时“立体”的体积V＝0)．

    (1)求V＝0的概率；
    (2)求V的分布列及数学期望E(V)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    寒假期间，我市某校学生会组织部分同学，用“10分制”随机调查“阳光花园”社区人们的幸福度，现从调查人群中随机抽取16名，如果所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）；若幸福度分数不低于8.5分，则该人的幸福度为“幸福”.

    （1）求从这16人中随机选取3人，至少有2人为“幸福”的概率；
    （2）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记表示抽到“幸福”的人数，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    对某电子元件进行寿命追踪调查，所得情况如右频率分布直方图.

    （1）图中纵坐标处刻度不清，根据图表所提供的数据还原；
    （2）根据图表的数据按分层抽样，抽取个元件，寿命为之间的应抽取几个；
    （3）从（2）中抽出的寿命落在之间的元件中任取个元件，求事件“恰好有一个寿命为，一个寿命为”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

    (1)分别求第3，4，5组的频率；
    (2)若该校决定在笔试成绩较高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
    (ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙恰有一人进入第二轮面试的概率；
    (ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试，设第4组中有名学生被考官L面试，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    若一批白炽灯共有10000只，其光通量X服从正态分布，其正态分布密度函数是f(x)＝，x∈(－∞，＋∞)，试求光通量在下列范围内的灯泡的个数．
    (1)(203,215)；(2)(191,227)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某计算机程序每运行一次都随机出现一个五位的二进制数A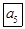＝，其中A的各位数中，a1＝1，ak(k＝2,3,4,5)出现0的概率为，出现1的概率为.记X＝a1＋a2＋a3＋a4＋a5，当程序运行一次时，
    (1)求X＝3的概率；
    (2)求X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两人破译一密码，它们能破译的概率分别为和，试求：
    (1)两人都能破译的概率；
    (2)两人都不能破译的概率；
    (3)恰有一人能破译的概率；
    (4)至多有一人能破译的概率；
    (5)若要使破译的概率为99%，至少需要多少乙这样的人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    小波以游戏方式决定是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋.

    (1)写出数量积X的所有可能取值;
    (2)分别求小波去下棋的概率和不去唱歌的概率.

    查看答案和解析>>

    同步练习册答案