
某地区因干旱缺水,政府向市民宣传节约用水,并进行广泛动员 三个月后,统计部门在一个小区随机抽取了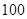 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)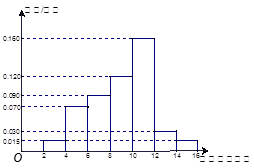
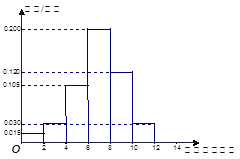
动员前 动员后
(Ⅰ)已知该小区共有居民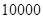 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是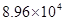 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
(Ⅱ)为了解动员前后市民的节水情况,媒体计划在上述家庭中,从政府动员前月均用水量在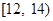 内的家庭中选出
内的家庭中选出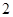 户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)利用频率分布直方图可求;(Ⅱ)按照分布列的取值情况求对应的概率即可
试题解析:(Ⅰ)根据直方图估计该小区在政府动员后平均每户居民的月均用水量为 (吨)
(吨)
于是可估计该小区在政府动员后比动员前平均每月可节约用水 (吨) 6分
(吨) 6分
(Ⅱ)由(Ⅰ)可知动员前月均用水量在 内的家庭有
内的家庭有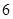 户,
户,
设为:甲、乙、 、
、 、
、 、
、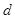 ,从中任选
,从中任选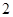 户,共包含
户,共包含 个基本事件:
个基本事件:
(甲,乙)、(甲, )、(甲,
)、(甲, )、(甲,
)、(甲, )、(甲,
)、(甲,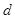 )、(乙,
)、(乙, )、(乙,
)、(乙, )、
)、
(乙, )、(乙,
)、(乙,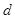 )、(
)、( ,
, )、(
)、( ,
, )、(
)、( ,
,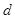 )、(
)、( ,
, )、(
)、( ,
,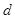 )、(
)、( ,
,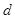 )
)
甲、乙两家恰好被选中是其中一个基本事件:(甲,乙),
因此所求概率为 12分
12分
考点:频率分布直方图、概率,考查数据处理、推理论证、运算求解能力和应用意识,以及或然与必然的数学思想


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:解答题
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。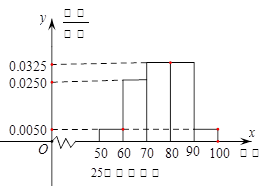
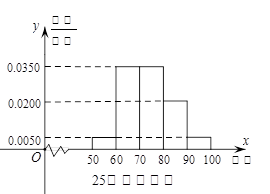
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.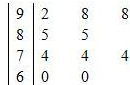
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从80分以上的样本中随机抽出2名学生,求抽出的2名学生的成绩分别在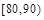 、
、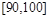 上的概率.
上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下: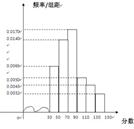
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为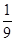 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 |  |
| B | 12 | 3 |
| C | 8 | 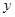 |
 与
与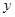 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)求出表中 、
、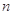 、
、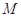 、
、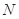 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
| 分组 | 频数 | 频率 |
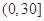 | 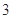 | 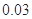 |
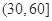 | 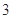 | 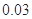 |
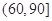 | 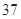 | 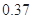 |
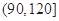 |  | 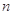 |
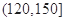 | 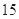 | 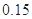 |
| 合计 | 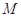 | 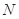 |

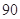 分以上的人数;
分以上的人数;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种报纸,进货商当天以每份进价 元从报社购进,以每份售价
元从报社购进,以每份售价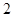 元售出。若当天卖不完,剩余报纸报社以每份
元售出。若当天卖不完,剩余报纸报社以每份 元的价格回收。根据市场统计,得到这个季节的日销售量
元的价格回收。根据市场统计,得到这个季节的日销售量 (单位:份)的频率分布直方图(如图所示),将频率视为概率。
(单位:份)的频率分布直方图(如图所示),将频率视为概率。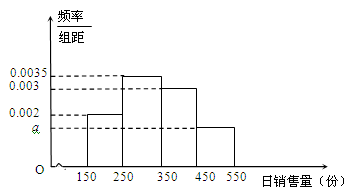
(Ⅰ)求频率分布直方图中 的值;
的值;
(Ⅱ)若进货量为 (单位:份),当
(单位:份),当

 时,求利润
时,求利润 的表达式;
的表达式;
(Ⅲ)若当天进货量 ,求利润
,求利润 的分布列和数学期望
的分布列和数学期望 (统计方法中,同一组数据常用该组区间的中点值作为代表).
(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com