
【题目】设f(x)=![]() (m>0,n>0).
(m>0,n>0).
(1) 当m=n=1时,求证:f(x)不是奇函数;
(2) 设f(x)是奇函数,求m与n的值;
(3) 在(2)的条件下,求不等式f(f(x))+f![]() <0的解集.
<0的解集.
【答案】(1)见解析(2)![]() (3)(-∞,log23).
(3)(-∞,log23).
【解析】试题分析:(1)只要举一个反例说明f(x)不是奇函数即可(2)由奇函数性质得恒等式,再根据恒等式定理得对应项系数为零,解方程组可得m与n的值;注意验证函数定义域关于零点对称(3)先分离函数,判定函数单调性,再利用奇偶性以及单调性化简不等式f(f(x))+f![]() <0为f(x)>-
<0为f(x)>-![]() ,最后最后为指数函数不等式: 2x<3,解得x<log23即为所求
,最后最后为指数函数不等式: 2x<3,解得x<log23即为所求
试题解析:(1) 证明:因为当m=n=1时,f(x)=![]() ,f(1)=-
,f(1)=-![]() ,f(-1)=
,f(-1)=![]() , f(-1)≠-f(1),所以f(x)不是奇函数.
, f(-1)≠-f(1),所以f(x)不是奇函数.
(2) 解:当f(x)是奇函数时,f(-x)=-f(x),即![]() =-
=-![]() 对定义域内任意实数x成立.
对定义域内任意实数x成立.
化简整理得(2m-n)·22x+(2mn-4)·2x+(2m-n)=0,这是关于x的恒等式,
所以![]()
所以![]() (不符,舍去)或
(不符,舍去)或![]()
经检验![]() 符合题意,所以
符合题意,所以![]()
(3) 解:由(2)可知f(x)=![]() =
=![]() (-1+
(-1+![]() ),易判断f(x)是R上单调减函数;
),易判断f(x)是R上单调减函数;
由f(f(x))+f(![]() )<0,得f(f(x))<f
)<0,得f(f(x))<f![]() f(x)>-
f(x)>-![]() 2x<3 x<log23,
2x<3 x<log23,
所以f(x)>0的解集为(-∞,log23).


科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() (
(![]() ,
,![]() )有公共焦点
)有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() ,
,![]() 在在第一象限的交点,且
在在第一象限的交点,且![]() .
.
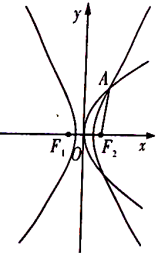
(1)求双曲线![]() 的方程;
的方程;
(2)以![]() 为圆心的圆
为圆心的圆![]() 与双曲线的一条渐进线相切,圆
与双曲线的一条渐进线相切,圆![]() .已知点
.已知点![]() ,过点
,过点![]() 作互相垂直分别与圆
作互相垂直分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 解得的弦长为
解得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .试探索
.试探索![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,M,N分别为AB,AC的中点,沿MN将△AMN折起,使点A到A′的位置.若平面A′MN与平面MNCB垂直,则四棱锥A′MNCB的体积为________.
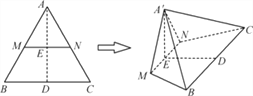
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
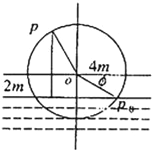
【题目】如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)已知椭圆C的中心在坐标原点,离心率![]() ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线![]() 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点![]() 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com