
【题目】已知函数f(x)=lnx+a(x2﹣3x+2),其中a为参数.
(1)当a=0时,求函数f(x)在x=1处的切线方程;
(2)讨论函数f(x)极值点的个数,并说明理由;
(3)若对任意x∈[1,+∞),f(x)≥0恒成立,求实数a的取值范围.
【答案】
(1)解:当a=0时,f(x)=lnx,f(1)=0,
求导f′(x)= ![]() ,f′(1)=1,
,f′(1)=1,
f(x)在x=1处的切线斜率k=1,则y﹣0=1×(x﹣1),整理得:y=x﹣1,;
∴函数f(x)在x=1处的切线方程y=x﹣1
(2)解:f(x)=lnx+a(x2﹣3x+2),定义域为(0,+∞) ![]() ,设g(x)=2ax2﹣3ax+1,
,设g(x)=2ax2﹣3ax+1,
①当a=0时,g(x)=1,故f'(x)>0,
∴f(x)在(0,+∞)上为增函数,所以无极值点
②当a>0时,△=9a2﹣8a,
若0<a≤ ![]() 时△≤0,g(x)≥0,故f'(x)≥0,故f(x)在(0,+∞)上递增,所以无极值点.
时△≤0,g(x)≥0,故f'(x)≥0,故f(x)在(0,+∞)上递增,所以无极值点.
若a> ![]() 时△>0,设g(x)=0的两个不相等的实数根为x1,x2,且x1<x2,
时△>0,设g(x)=0的两个不相等的实数根为x1,x2,且x1<x2,
且 ![]() ,而g(0)=1>0,则
,而g(0)=1>0,则 ![]() ,
,
所以当x∈(0,x1),g(x)>0,f'(x)>0,f(x)单调递增;
当x∈(x1,x2),g(x)<0,f'(x)<0,f(x)单调递减;
当x∈(x2,+∞),g(x)>0,f′(x)>0,f(x)单调递增.
所以此时函数f(x)有两个极值点;
③当a<0时△>0,设g(x)=0的两个不相等的实数根为x1,x2,且x1<x2,
但g(0)=1>0,所以x1<0<x2,
所以当x∈(0,x2),g(x)>0,f'(x)>0,f(x)单调递増;
当x∈(x2,+∞),g(x)<0,f′(x)<0,f(x)单调递减.
所以此时函数f(x)只有一个极值点.
综上得:
当a<0时f(x)有一个极值点;
当0≤a≤ ![]() 时f(x)的无极值点;
时f(x)的无极值点;
当a> ![]() 时,f(x)的有两个极值点
时,f(x)的有两个极值点
(3)解:方法一:当0≤a≤ ![]() 时,由(2)知f(x)在[1,+∞)上递增,
时,由(2)知f(x)在[1,+∞)上递增,
所以f(x)≥f(1)=0,符合题意;
当 ![]() <a≤1时,g(1)=1﹣a≥0,x2≤1,f(x)在[1,+∞)上递增,所以f(x)≥f(1)=0,符合题意;
<a≤1时,g(1)=1﹣a≥0,x2≤1,f(x)在[1,+∞)上递增,所以f(x)≥f(1)=0,符合题意;
当a>1时,g(1)=1﹣a<0,x2>1,所以函数f(x)在(1,x2)上递减,所以f(x)<f(1)=0,不符合题意;
当a<0时,由(1)知lnx≤x﹣1,于是f(x)=lnx+a(x2﹣3x+2)≤x﹣1+a(x2﹣3x+2)
当 ![]() 时,x﹣1+a(x2﹣3x+2)<0,此时f(x)<0,不符合题意.
时,x﹣1+a(x2﹣3x+2)<0,此时f(x)<0,不符合题意.
综上所述,a的取值范围是0≤a≤1.
方法二:g(x)=2ax2﹣3ax+1,注意到对称轴为 ![]() ,g(1)=1﹣a,
,g(1)=1﹣a,
当0≤a≤1时,可得g(x)≥0,故f(x)在[1,+∞)上递增,所以f(x)≥f(1)=0,符合题意;
当a>1时,g(1)=1﹣a<0,x2>1,所以函数f(x)在(1,x2)上递减,此时f(x)<f(1)=0,不符合题意;
当a<0时,由(1)知lnx≤x﹣1,于是f(x)=lnx+a(x2﹣3x+2)≤x﹣1+a(x2﹣3x+2)
当 ![]() 时,x﹣1+a(x2﹣3x+2)<0,此时f(x)<0,不符合题意.
时,x﹣1+a(x2﹣3x+2)<0,此时f(x)<0,不符合题意.
综上所述,s的取值范围是0≤a≤1
【解析】(1)根据导数的几何意义,求得切线的斜率,利用点斜式方程,即可求得函数f(x)在x=1处的切线方程;(2)求导,分类讨论,根据导数与函数单调性及极值的关系,分别求得函数f(x)极值点的个数;(3)方法一:由(2)可知:分类讨论,根据函数的单调性,求得f(x)的最值,即可求得a的取值范围; 方法二:设g(x)=2ax2﹣3ax+1,根据二次函数的性质,分类讨论,即可求得实数a的取值范围.
【考点精析】关于本题考查的函数的极值与导数,需要了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面三个类比结论:①向量 ![]() ,有
,有 ![]() ;类比复数
;类比复数 ![]() ,有
,有 ![]() ;
;
②实数 ![]() 、
、 ![]() 有
有 ![]() ;类比向量
;类比向量 ![]() ,有
,有 ![]() ;
;
③实数 ![]() 、
、 ![]() 有
有 ![]() ,则
,则 ![]() ;类比复数
;类比复数 ![]() ,有
,有 ![]() ,则
,则 ![]() .其中类比结论正确的命题个数为 ( )
.其中类比结论正确的命题个数为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第 ![]() 个图形包含
个图形包含 ![]() 个小正方形.
个小正方形.
(Ⅰ)求出 ![]() ;
;
(Ⅱ)利用合情推理的“归纳推理思想”归纳出 ![]() 与
与 ![]() 的关系式,并根据你得到的关系式求
的关系式,并根据你得到的关系式求 ![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,an=cos ![]() (n∈N*)
(n∈N*)
(1)试将an+1表示为an的函数关系式;
(2)若数列{bn}满足bn=1﹣ ![]() (n∈N*),猜想an与bn的大小关系,并证明你的结论.
(n∈N*),猜想an与bn的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( ) 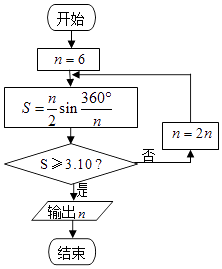
A.48
B.36
C.30
D.24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com