
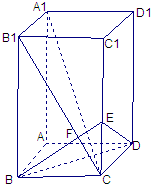
 如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F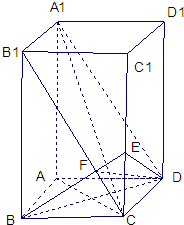 解法一:
解法一: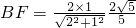 …(9分)
…(9分)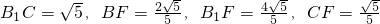
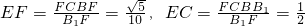
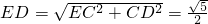
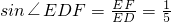 …..(14分)
…..(14分)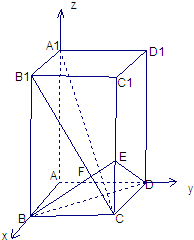
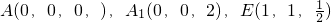 B(1,0,0),D(0,1,0),C(1,1,0)
B(1,0,0),D(0,1,0),C(1,1,0)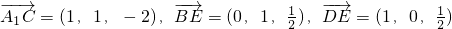
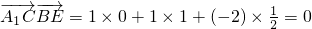 ,
,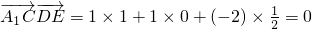
 ,
,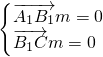 ,
,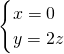 ,
,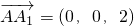 ,
,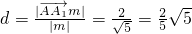 …(9分)
…(9分)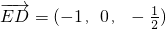 ,
,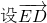 与m所成角为θ,
与m所成角为θ,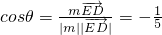
 ….(14分)
….(14分)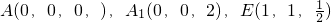 ,B(1,0,0),D(0,1,0),C(1,1,0),由向量法能证明A1C⊥平面EBD.
,B(1,0,0),D(0,1,0),C(1,1,0),由向量法能证明A1C⊥平面EBD.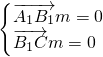 ,所以m=(0,2,1),由此能求出点A到平面A1B1C的距离.
,所以m=(0,2,1),由此能求出点A到平面A1B1C的距离.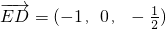 ,
,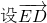 与m所成角为θ,由
与m所成角为θ,由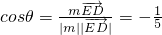 ,能求出直线ED与平面A1B1C所成角的正弦值.
,能求出直线ED与平面A1B1C所成角的正弦值.

科目:高中数学 来源: 题型:
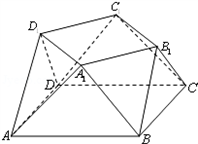
 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4
如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4| 2 |
查看答案和解析>>
科目:高中数学 来源:大纲版2012届高三上学期单元测试(9)数学试题 题型:044
如图,已知长方体ABCD-A1B1C1D1中,AB1=2,AA1=AD=1,求:
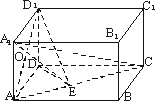
(1)点D1到直线AC的距离;
(2)直线AB与面A1DC的距离;
(3)异面直线A1D与B1C1的距离.
查看答案和解析>>
科目:高中数学 来源:安徽省模拟题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012年山东省普通高中学业水平考试数学样卷(三)(解析版) 题型:解答题
 ,P为CC1的中点,AC、BD交于O
,P为CC1的中点,AC、BD交于O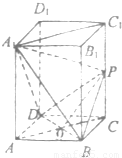
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com