
【题目】如图,在三棱柱![]() 中,
中, ![]() 侧面
侧面![]() 底面
底面![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析: (1)由四边形![]() 为菱形,得对角线
为菱形,得对角线![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 侧面
侧面![]() B1,从而
B1,从而![]() 1,由此能证明
1,由此能证明![]() 平面
平面![]() ;
;
(2)由勾股定理得![]() ,由菱形
,由菱形![]() 中
中![]() ,得
,得![]() 为正三角形,以菱形
为正三角形,以菱形![]() 的对角线交点
的对角线交点![]() 为坐标原点
为坐标原点![]() 方向为
方向为![]() 轴,
轴, ![]() 方向为
方向为![]() 轴,过
轴,过![]() 且与
且与![]() 平行的方向为
平行的方向为![]() 轴建立如图空间直角坐标系,分别求出平面
轴建立如图空间直角坐标系,分别求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,由此能求出二面角
的法向量,由此能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:在侧面![]() 中,
中,
![]() ,
,
![]() 四边形
四边形![]() 为菱形,
为菱形,
![]() 对角线
对角线![]() .
.
![]() 侧面
侧面![]() 底面
底面![]() ,
,
![]() 侧面
侧面![]() ,
,
![]() .
.
又![]() ,
,
![]() 平面
平面![]() .
.
(2)在![]() 中,
中, ![]() ,
,
又菱形![]() 中,
中, ![]() ,
,
![]() 为正三角形.
为正三角形.
如图,以菱形![]() 的对角线交点
的对角线交点![]() 为坐标原点
为坐标原点![]() 方向为
方向为![]() 轴,
轴, ![]() 方向为
方向为![]() 轴,过
轴,过![]() 且与
且与![]() 平行的方向为
平行的方向为![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
则![]()
![]() ,
,
设![]() 为平面
为平面![]() 的方向量,则
的方向量,则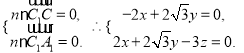
令![]() ,得
,得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
又![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
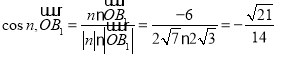 .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的等边三角形,四边形
是边长为3的等边三角形,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,点
,点![]() 为
为![]() 上的一点,且
上的一点,且![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
① 向左平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
② 向右平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
③ 每个点的横坐标缩短为原来的![]() ,向右平移
,向右平移![]() 个单位长度;
个单位长度;
④ 每个点的横坐标缩短为原来的![]() ,向左平移
,向左平移![]() 个单位长度;
个单位长度;
其中能将![]() 的图像变换成函数
的图像变换成函数![]() 的图像的是( )
的图像的是( )
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底,
为自然对数的底, ![]() )的导函数为
)的导函数为![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)设点![]() ,
, ![]() 是函数
是函数![]() 图象上两点,若对任意的
图象上两点,若对任意的![]() ,割线
,割线![]() 的斜率都大于
的斜率都大于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com