
【题目】已知函数![]()
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1
①若函数G(x)有两相异零点且![]() 在
在![]() 上是减函数,求实数m的取值范围。
上是减函数,求实数m的取值范围。
②是否存在整数a,b使得![]() 的解集恰好为
的解集恰好为![]() 若存在,求出a,b的值,若不存在,请说明理由。
若存在,求出a,b的值,若不存在,请说明理由。
【答案】(1)详见解析;(2)①(﹣∞,0]∪[2,+∞);②![]() 或
或![]() .
.
【解析】
(1)判断对应方程的△与0的关系,易得结论;
(2)由函数f(x)=mx+3,g(x)=x2+2x+m,我们易给出函数G(x)=f(x)﹣g(x)﹣1,①若|G(x)|在[﹣1,0]上是减函数,根据对折变换函数图象的特征,我们分△≤0和△>0两种情况进行讨论,可得到满足条件的m的取值范围;②若a≤G(x)≤b的解集恰好是[a,b],则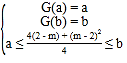 将a,b代入消去m,可以求出a,b的值.
将a,b代入消去m,可以求出a,b的值.
证明:(1)f(x)﹣g(x)=﹣x2+(m﹣2)x+3﹣m.
令f(x)﹣g(x)=0.
则△=(m﹣2)2﹣4(m﹣3)=m2﹣8m+16=(m﹣4)2≥0恒成立.
所以方程f(x)﹣g(x)=0有解.
所以函数f(x)﹣g(x)必有零点.
(2)①G(x)=f(x)﹣g(x)﹣1=﹣x2+(m﹣2)x+2﹣m.
①令G(x)=0,△=(m﹣2)2﹣4(m﹣2)=(m﹣2)(m﹣6).
当△≤0,即2≤m≤6时,G(x)=﹣x2+(m﹣2)x+2﹣m≤0恒成立,
所以|G(x)|=x2﹣(m﹣2)x+m﹣2.
因为|G(x)|在[﹣1,0]上是减函数,所以![]() 0.解得m≥2.
0.解得m≥2.
所以2≤m≤6.
当△>0,即m<2或m>6时,|G(x)|=|x2﹣(m﹣2)x+m﹣2|.
因为|G(x)|在[﹣1,0]上是减函数,
所以方程x2﹣(m﹣2)x+m﹣2=0的两根均大于零或一根大于零另一根小于零
且x![]() 1.
1.
所以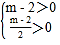 或
或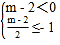
解得m>2或m≤0.
所以m≤0或m>6.
综上可得,实数m的取值范围为(﹣∞,0]∪[2,+∞).
②因为a≤G(x)≤b的解集恰好是[a,b],
所以![]()
由![]()
消去m,得ab﹣2a﹣b=0,显然b≠2.
所以a![]() 1
1![]() .
.
因为a,b均为整数,所以b﹣2=±1或b﹣2=±2.
解得![]() 或
或![]() 或
或![]() 或
或![]() 因为a<b,且a
因为a<b,且a![]() b
b
所以![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同![]() 直线
直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() 为参数
为参数![]() ,设直线l与曲线C交于A,B两点.
,设直线l与曲线C交于A,B两点.
![]() 写出直线
写出直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
![]() 已知点P在曲线C上运动,求点P到直线
已知点P在曲线C上运动,求点P到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为2,左右焦点分别为
的焦距为2,左右焦点分别为![]() ,
,![]() ,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线
,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线![]() 相切.
相切.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设不过原点的直线l:
设不过原点的直线l:![]() 与椭圆C交于A,B两点.
与椭圆C交于A,B两点.
![]() 若直线
若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线l过定点,并求出该定点的坐标;
,求证:直线l过定点,并求出该定点的坐标;
![]() 若直线l的斜率是直线OA,OB斜率的等比中项,求
若直线l的斜率是直线OA,OB斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.


(1)求证: ![]()
![]() ;
;
(2)![]() ;
;
(3)设![]() 为
为![]() 中点,在
中点,在![]() 边上找一点
边上找一点![]() ,使
,使![]() //平面
//平面![]() 并求
并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对正在进行的一项教学改革的态度,从500名高一学生和400名高二学生中按分层抽样的方式抽取了45名学生进行问卷调查,结果可以分成以下三类:支持、反对、无所谓,调查结果统计如下:
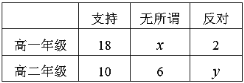
(1)(i)求出表中的![]() 的值;
的值;
(ii)从反对的同学中随机选取2人进一步了解情况,求恰好高一、高二各1人的概率;
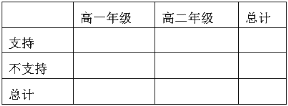
(2)根据表格统计的数据,完成下面的![]() 的列联表,并判断是否有90%的把握认为持支持与就读年级有关.(不支持包括无所谓和反对)
的列联表,并判断是否有90%的把握认为持支持与就读年级有关.(不支持包括无所谓和反对)
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
(1)为了调查评委对7位歌手的支持情况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取了6人,请将其余各组抽取的人数填入下表.
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | 6 |
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com