
【题目】如图,![]() 、
、![]() 是双曲线
是双曲线![]() 的两个焦点,一条直线与双曲线的右支相切,且分别交两条渐近线于A、B.又设O为坐标原点,求证: (1)
的两个焦点,一条直线与双曲线的右支相切,且分别交两条渐近线于A、B.又设O为坐标原点,求证: (1)![]() ; ⑵
; ⑵![]() 、
、![]() 、A、B四点在同一个圆上.
、A、B四点在同一个圆上.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】近年来大气污染防治工作得到各级部门的重视,某企业在现有设备下每日生产总成本![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)之间的函数关系式为
(单位:吨)之间的函数关系式为![]() ,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为
,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为![]() 万元,除尘后当日产量
万元,除尘后当日产量![]() 时,总成本
时,总成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每吨产品出厂价为48万元,试求除尘后日产量为多少时,每吨产品的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
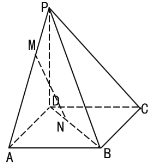
【题目】如图,四棱锥P-ABCD底面为正方形,PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
(1)求证:直线MN∥平面PCD.
(2)若点M为线段PA的中点,求直线PB与平面AMN所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+![]() ﹣1,a∈R.
﹣1,a∈R.
(1)当a>0时,若函数f(x)在区间[1,3]上的最小值为![]() ,求a的值;
,求a的值;
(2)讨论函数g(x)=f′(x)﹣![]() 零点的个数.
零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为4的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)判断在线段![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com