
分析 (1)当k=0时,利用换元法设t=sinx-cosx,结合基本不等式的性质即可求y=f(x)的值域;
(2)利用换元法和参数分离法,结合一元二次函数的性质求出函数f(x)的最小值即可得到结论.
解答 解:(1)当k=0时,f(x)=$\frac{2-sin2x}{sinx-cosx}$,
设t=sinx-cosx,则t2=1-2sinxcosx=1-sin2x,
即sin2x=1-t2,
∵t=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$),
∴当x∈[$\frac{5π}{12}$,π]时,x-$\frac{π}{4}$∈[$\frac{π}{6}$,$\frac{3π}{4}$].
∴sin(x-$\frac{π}{4}$)∈[$\frac{1}{2}$,1].
即$\sqrt{2}$sin(x-$\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$].
即t∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$].
则函数等价为y=g(t)=$\frac{2-1+{t}^{2}}{t}=\frac{1+{t}^{2}}{t}$=t+$\frac{1}{t}$,
∵g(t)=t+$\frac{1}{t}$在[$\frac{\sqrt{2}}{2}$,1]上递减,则[1,$\sqrt{2}$]上递增,
∴g(t)的最小值为g(1)=1+1=2,
∵g($\sqrt{2}$)=$\sqrt{2}$+$\frac{1}{\sqrt{2}}$=$\sqrt{2}$+$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$,
g([$\frac{\sqrt{2}}{2}$)=$\frac{\sqrt{2}}{2}$+$\frac{1}{\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}}{2}$+$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$,
∴2≤y≤$\frac{3\sqrt{2}}{2}$,
即函数的值域为[2,$\frac{3\sqrt{2}}{2}$].
(2)若k>0,则f(x)=$\frac{k+2-sin2x}{sinx-cosx}$等价为y=$\frac{k+2+{t}^{2}-1}{t}$=$\frac{k+1}{t}$+t≥2$\sqrt{t•\frac{k+1}{t}}$=2$\sqrt{k+1}$,
若不等式f(x)≥3恒成立,
即$\frac{k+1}{t}$+t≥3,
即k+1+t2≥3t,
即k≥-t2+3t-1,
设g(t)=-t2+3t-1,
则g(t)=-(t-$\frac{3}{2}$)2+$\frac{5}{4}$,
∵t∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$].
∴函数在t∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$]上为增函数,
∴当t=$\sqrt{2}$时,g(t)取得最大值,为g($\sqrt{2}$)=-2+3$\sqrt{2}$-1=3$\sqrt{2}-3$.
即k≥3$\sqrt{2}-3$.
点评 本题主要考查函数最值的应用,利用换元法结合三角函数的有界性,结合基本不等式求出函数的最值是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
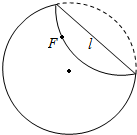 准备一张圆形纸片,在圆内任取不同于圆心的一点F,将纸片折起,使圆周过点F(如图),然后将纸片展开,就得到一条折痕L(为了看清楚,可以把直线L画出来),这样继续下去得到若干折痕.观察这些折痕围成的轮廓,它们形成了什么曲线?
准备一张圆形纸片,在圆内任取不同于圆心的一点F,将纸片折起,使圆周过点F(如图),然后将纸片展开,就得到一条折痕L(为了看清楚,可以把直线L画出来),这样继续下去得到若干折痕.观察这些折痕围成的轮廓,它们形成了什么曲线?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:选择题
已知向量 =(m,4),
=(m,4), =(3,-2),且
=(3,-2),且 ∥
∥ ,则m=( )
,则m=( )
A.6 B.-6 C. 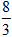 D.
D. 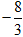
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com