
【题目】如图,过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,记以
两点,记以![]() ,
,![]() 为直径端点的圆为圆
为直径端点的圆为圆![]() .
.
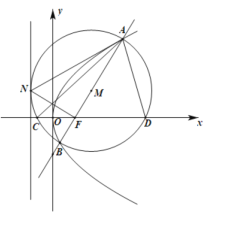
(1)证明:圆![]() 与抛物线的准线相切;
与抛物线的准线相切;
(2)设![]() ,点
,点![]() 在焦点的右侧,圆
在焦点的右侧,圆![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,记
两点,记![]() 和
和![]() 的面积为
的面积为![]() ,
,![]() 求
求![]() 的最大值(其中,点
的最大值(其中,点![]() 为圆
为圆![]() 与抛物线准线的切点)
与抛物线准线的切点)
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() (
(![]() 为参数),直线
为参数),直线![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于在
交于在![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|lnx|,若函数g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
A. (0,![]() )B. (
)B. (![]() ,e)C. (
,e)C. (![]() ,
,![]() )D. (0,
)D. (0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线C1的参数方程为![]() (t为参数,0<α<π),曲线C2的参数方程为
(t为参数,0<α<π),曲线C2的参数方程为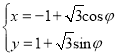 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C2的极坐标方程;
(2)设曲线C1与曲线C2的交点分别为A,B,M(﹣2,0),求|MA|2+|MB|2的最大值及此时直线C1的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) | [200,+∞) |
顾客人数 | m | 20 | 30 | n | 10 |
统计结果显示100位顾客中购物款不低于100元的顾客占60%,据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件).(注:视频率为概率)
(1)试确定![]() 的值,并估计该商场每日应准备纪念品的数量;
的值,并估计该商场每日应准备纪念品的数量;
(2)为了迎接店庆,商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物
款小于200元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) |
返利百分比 | 0 | 6% | 8% | 10% |
估计该商场日均让利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com