
【题目】已知椭圆 ![]() =1(a>b>0)的一个顶点为A(0,1),离心率为
=1(a>b>0)的一个顶点为A(0,1),离心率为 ![]() ,过点B(0,﹣2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2 .
,过点B(0,﹣2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2 .
(1)求椭圆的方程;
(2)求△CDF2的面积.
【答案】
(1)解:∵椭圆 ![]() =1(a>b>0)的一个顶点为A(0,1),离心率为
=1(a>b>0)的一个顶点为A(0,1),离心率为 ![]() ,
,
∴b= ![]() =1,且
=1,且 ![]() =
= ![]() ,解之得a=
,解之得a= ![]() ,c=1
,c=1
可得椭圆的方程为 ![]()
(2)解:∵左焦点F1(﹣1,0),B(0,﹣2),得F1B直线的斜率为﹣2
∴直线F1B的方程为y=﹣2x﹣2
由 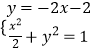 ,化简得9x2+16x+6=0.
,化简得9x2+16x+6=0.
∵△=162﹣4×9×6=40>0,
∴直线与椭圆有两个公共点,设为C(x1,y1),D(x2,y2),
则 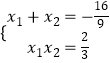
∴|CD|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]()
又∵点F2到直线BF1的距离d= ![]() =
= ![]() ,
,
∴△CDF2的面积为S= ![]() |CD|×d=
|CD|×d= ![]()
![]() ×
× ![]() =
= ![]()
【解析】(1)根据椭圆的基本概念和平方关系,建立关于a、b、c的方程,解出a= ![]() ,b=c=1,从而得到椭圆的方程;(2)求出F1B直线的斜率得直线F1B的方程为y=﹣2x﹣2,与椭圆方程联解并结合根与系数的关系算出|x1﹣x2|=
,b=c=1,从而得到椭圆的方程;(2)求出F1B直线的斜率得直线F1B的方程为y=﹣2x﹣2,与椭圆方程联解并结合根与系数的关系算出|x1﹣x2|= ![]() ,结合弦长公式可得|CD|=
,结合弦长公式可得|CD|= ![]()
![]() ,最后利用点到直线的距离公式求出F2到直线BF1的距离d,即可得到△CDF2的面积.
,最后利用点到直线的距离公式求出F2到直线BF1的距离d,即可得到△CDF2的面积.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设a∈R,函数f(x)=x|x﹣a|+2x.
(1)若a=3,求函数f(x)在区间[0,4]上的最大值;
(2)若存在a∈(2,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数解,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0),及⊙C:x2+y2﹣6x+4y+4=0.
(1)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(2)设过点P的直线与⊙C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知an=log(n+1)(n+2)(n∈N*).我们把使乘积a1a2a3…an为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
A.1024
B.2003
C.2026
D.2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一企业从某生产线上随机抽取40件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数表
,得到如下的频数表
|
|
|
|
|
频数 | 3 | 15 | 17 | 5 |
(1)估计该技术指标值的平均数(以各组区间中点值为代表);
(2)若![]() ,则该产品不合格,其余合格产品。产生一件产品,若是合格品,可盈利100元,若不是合格品则亏损20元。从该生产线生产的产品中任取2件,记
,则该产品不合格,其余合格产品。产生一件产品,若是合格品,可盈利100元,若不是合格品则亏损20元。从该生产线生产的产品中任取2件,记![]() 为这2件产品的总利润,求随机变量
为这2件产品的总利润,求随机变量![]() 的分布列和期望值。
的分布列和期望值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC中角A,B,C的对边,且csinB= ![]() bcosC.
bcosC.
(1)求角C的大小;
(2)若c=3,sinA=2sinB,求△ABC的面积S△ABC .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com