
分析 由已知设点P(a,a),由P(a,a)到原点的距离等于它到点Q(4$\sqrt{3}$,0)的距离,利用两点间距离公式得$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{(a-4\sqrt{3})^{2}+{a}^{2}}$,由此能求出点P的坐标.
解答 解:∵点P在直角坐标系第一、三象限的角平分线上,∴设点P(a,a),
∵P(a,a)到原点的距离等于它到点Q(4$\sqrt{3}$,0)的距离,
∴$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{(a-4\sqrt{3})^{2}+{a}^{2}}$,
解得a=2$\sqrt{3}$.
∴P(2$\sqrt{3}$,2$\sqrt{3}$).
故答案为:(2$\sqrt{3}$,2$\sqrt{3}$).
点评 本题考查满足条件的点的坐标的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$共线,$\overrightarrow{b}$与$\overrightarrow{c}$共线,则$\overrightarrow{a}$与$\overrightarrow{c}$也共线 | |
| B. | 任意两个相等的非零向量的始点与终点总是一平行四边形的四个顶点 | |
| C. | 向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线,则$\overrightarrow{a}$与$\overrightarrow{b}$都是非零向量 | |
| D. | 有相同起点的两个非零向量不平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
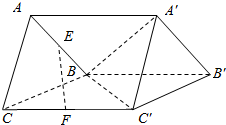 如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com