
【题目】如图,在折线![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,若折线上满足条件
的中点,若折线上满足条件![]() 的点
的点![]() 至少有
至少有![]() 个,则实数
个,则实数![]() 的取值范围是___________.
的取值范围是___________.

【答案】![]()
【解析】
以BC的垂直平分线为y轴,以BC为x轴,建立如图所示的平面直角坐标系,分别表示各个点的坐标,设P(x,y),根据向量的数量积可得当k+9>0时,点P的轨迹为以(0,![]() )为圆心,以
)为圆心,以![]() 为半径的圆,结合图象,即可求出满足条件
为半径的圆,结合图象,即可求出满足条件![]() 的点P至少有4个的k的取值范围.
的点P至少有4个的k的取值范围.
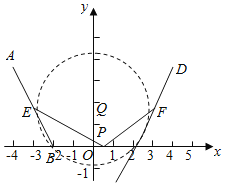
解:以BC的垂直平分线为y轴,以BC为x轴,建立如图所示的平面直角坐标系,
∵AB=BC=CD=4,∠ABC=∠BCD=120°,
∴B(﹣2.0),C(2,0),A(﹣4,2![]() ),D(4,2
),D(4,2![]() ),
),
∵E、F分别是AB、CD的中点,
∴E(﹣3,![]() ),F(3,
),F(3,![]() ),
),
设P(x,y),﹣4≤x≤4,0≤y≤2![]() ,
,
∵![]() ,
,
∴(﹣3﹣x,![]() (3﹣x,
(3﹣x,![]() y)=
y)=![]() ,
,
即![]() ,
,
当k+9>0时,点P的轨迹为以(0,![]() )为圆心,以
)为圆心,以![]() 为半径的圆,
为半径的圆,
当圆与直线DC相切时,此时圆的半径r![]() ,此时点有2个,
,此时点有2个,
当圆经过点C时,此时圆的半径为r![]() ,此时点P有4个,
,此时点P有4个,
∵满足条件![]() 的点P至少有4个,结合图象可得,
的点P至少有4个,结合图象可得,
∴![]() k+9≤7,
k+9≤7,
解得![]() k≤﹣2,
k≤﹣2,
故实数k的取值范围为[![]() ,﹣2],
,﹣2],
故答案为:[![]() ,﹣2]
,﹣2]


科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为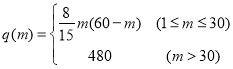 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值;
的值;
(3)若对任意实数![]() 、
、![]() 、
、![]() ,均存在以
,均存在以![]() 、
、![]() 、
、![]() 为三边边长的三角形,求实数
为三边边长的三角形,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知在平面直角坐标系xOy中,O为坐标原点,曲线C: 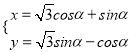 (α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ
(α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)曲线C上恰好存在三个不同的点到直线l的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司举办捐步公益活动,参与者通过捐赠每天的运动步数获得公司提供的牛奶,再将牛奶捐赠给留守儿童.此活动不但为公益事业作出了较大的贡献,公司还获得了相应的广告效益.据测算,首日参与活动人数为![]() 人,以后每天人数比前一天都增加
人,以后每天人数比前一天都增加![]() ,
,![]() 天后捐步人数稳定在第
天后捐步人数稳定在第![]() 天的水平,假设此项活动的启动资金为
天的水平,假设此项活动的启动资金为![]() 万元,每位捐步者每天可以使公司收益
万元,每位捐步者每天可以使公司收益![]() 元(以下人数精确到
元(以下人数精确到![]() 人,收益精确到
人,收益精确到![]() 元).
元).
(1)求活动开始后第![]() 天的捐步人数,及前
天的捐步人数,及前![]() 天公司的捐步总收益;
天公司的捐步总收益;
(2)活动开始第几天以后公司的捐步总收益可以收回启动资金并有盈余?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
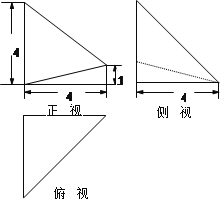
已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:
(i)老年人的人数多于中年人的人数;
(ii)中年人的人数多于青年人的人数;
(iii)青年人的人数的两倍多于老年人的人数.
①若青年人的人数为4,则中年人的人数的最大值为___________.
②抽取的总人数的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com