【题目】已知函数
(1)求函数
的单调递增区间；
(2)
内角
的对边分别为
，若
，
，
，且
，试求角
和角
.
【答案】（1）
（2）
【解析】
（1）将
解析式第一项利用两角和与差的余弦函数公式及特殊角的三角函数值化简，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，由正弦函数的递增区间列出关于x的不等式，求出不等式的解集即可得到的递增区间；
（2）由（1）确定的解析式，及
求出
的值，由B为三角形的内角，利用特殊角的三角函数值求出B的度数，再由b与c的值，利用正弦定理求出
的值，由C为三角形的内角，利用特殊角的三角函数值求出C的度数，由a大于b得到A大于B，检验后即可得到满足题意的B和C的度数.
（1）
，
令
，解得
故函数的递增区间为.
（2）
，
，
由正弦定理得：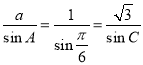
，
，
，
或
.
当
时，
：当
时，
（不合题意，舍）
所以.
科目：高中数学 来源： 题型：
【题目】甲乙两人参加某种选拔测试，在备选的10道题中，甲答对其中每道题的概率都是
，乙能答对其中的8道题，规定每次考试都从备选的10道题中随机抽出4道题进行测试，只有选中的4个题目均答对才能入选.
（1）求甲恰有2个题目答对的概率；
（2）求乙答对的题目数X的分布列；
（3）试比较甲，乙两人平均答对的题目数的大小，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将曲线
上每个点的横坐标伸长为原来的
倍(纵坐标不变),得到
的图象,则下列说法正确的是（ ）
A.的图象关于直线
对称
B.在
上的值域为
C.的图象关于点
对称
D.的图象可由
的图象向右平移
个单位长度得到
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：万元）对年销售量
（单位：吨）和年利润
（单位：万元）的影响．对近六年的年宣传费
和年销售量
（
）的数据作了初步统计，得到如下数据：
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟，发现年宣传费（万元）与年销售量（吨）之间近似满足关系式
（
）．对上述数据作了初步处理，得到相关的值如表：
|
|
|
|
|
|
|
|
（1）根据所给数据，求关于的回归方程；
（2）已知这种产品的年利润与，的关系为
若想在
年达到年利润最大，请预测年的宣传费用是多少万元？
附：对于一组数据
，
，…，
，其回归直线
中的斜率和截距的最小二乘估计分别为
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于定义域为
的函数
，如果同时满足以下三个条件：①任意的
，总有
；②
；③若
，
，
，总有
成立,则称函数
为理想函数.
（1）证明：若函数为理想函数，则
；
（2）证明：函数
，是理想函数；
（3）证明：若函数为理想函数，假定存在
，使得
且
，则
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
