
【题目】某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
经长期观察,y=f(t)的曲线可以近似地看成函数![]() 的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
(1)求y与t满足的函数关系式;
(2)某船吃水深度(船底离水面的距离)为6.5m,如果该船希望在同—天内安全进出港,请问该船在什么时间段能够安全进港?它同一天内最多能在港内停留多少小时?(忽略进 出港所需的时间).
【答案】(1)![]() (2)该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时.
(2)该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时.
【解析】 试题分析:(1)由表得周期![]() ,可求出
,可求出![]() ,由最大值和最小值可得
,由最大值和最小值可得![]() 和
和![]() ,故而可得解析式;(2)由题意计算出水深应不小于11.5,列出不等式
,故而可得解析式;(2)由题意计算出水深应不小于11.5,列出不等式![]() ,解不等式即可.
,解不等式即可.
试题解析:(1)由已知数据,易知y =f(t)的周期T=12,则![]() .
.
再由![]() ,得振幅A=3,b=10,
,得振幅A=3,b=10,
所以![]() .
.
(2)由题意,该船进出港时,水深应不小于5+6.5=11.5(米),
所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
在同一天内,取k=0或1,所以1≤t≤5或13≤t≤17,故进港时间为1:00~5:00或 13:00-17:00.所以该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 、
、 ![]() ,短轴两个端点为
,短轴两个端点为 ![]() 、
、 ![]() ,且四边形
,且四边形 ![]() 是边长为2的正方形.
是边长为2的正方形.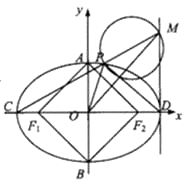
(1)求椭圆的方程;
(2)若 ![]() 、
、 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问 ![]() 轴上是否存异于点
轴上是否存异于点 ![]() 的定点
的定点 ![]() ,使得以
,使得以 ![]() 为直径的圆恒过直线
为直径的圆恒过直线 ![]() 、
、 ![]() 的交点,若存在,求出点
的交点,若存在,求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣alnx+x(a∈R)
(Ⅰ)当a=1时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(Ⅱ)讨论函数y=f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)= ![]() +bx(a≠0)
+bx(a≠0)
(Ⅰ)若a=﹣2时,函数h(x)=f(x)﹣g(x)在其定义域内是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设φ(x)=e2x+bex , x∈[0,ln2],求函数φ(x)的最小值;
(Ⅲ)设函数f(x)的图象C1与函数g(x)的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形 ABCD 中,对角线 AC 与 BD 相交于一点 O,∠A=60°,将△BDC 沿着 BD 折起得△BDC',连结 AC'.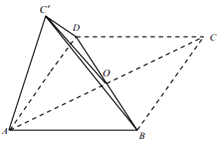
(Ⅰ)求证:平面 AOC'⊥平面 ABD;
(Ⅱ)若点 C'在平面 ABD 上的投影恰好是△ABD 的重心,求直线 CD 与底面 ADC'所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC=a,AC=b,且a,b是方程![]() 的两根,2cos(A+B)=1.
的两根,2cos(A+B)=1.
(1)求∠C的度数;
(2)求AB的长;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com