
分析 化简集合A、B,求出(1)a=-1时,集合B以及∁RB,计算A∩(∁RB)即可;
(2)讨论a的值,求出对应的集合B,以及A∩B=∅成立时a的取值范围.
解答 解:集合A={x|x2-6x+8<0}={x|(x-2)(x-4)<0}={x|2<x<4},
B={x|x2-4ax+3a2<0}={x|(x-a)(x-3a)<0};
(1)当a=-1时,B={x|-3<x<-1},
∴∁RB={x|x≤-3或x≥-1},
∴A∩(∁RB)={x|2<x<4};
(2)①当a=0时,集合B=∅,A∩B=∅成立,∴a=0;
②当a>0时,集合B={x|a<x<3a},
要使A∩B=∅成立,则有3a≤2或a≥4,
解得a≤$\frac{2}{3}$或a≥4,即0<a≤$\frac{2}{3}$或a≥4;
③当a<0时,集合B={x|3a<x<a},
要使A∩B=∅,则有3a≥4或a≤2,
解得a≥$\frac{4}{3}$或a≤2,即a<0;
综上,实数a的取值范围是{a|a≤$\frac{2}{3}$或a≥4}.
点评 本题考查了交、并、补集的混合运算,以及集合间的包含关系判断及应用,也考查了分类讨论思想的应用问题,熟练掌握各自的定义是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$和y=$(\sqrt{x})^{2}$ | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logx | D. | y=x和y=logaax |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
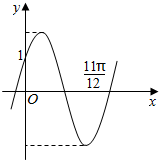 函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示
函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com