
【题目】已知![]() ,设实数
,设实数![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足
(i)![]() 、
、![]() 、
、![]() 且不全为0;
且不全为0;
(ii)![]() 、
、![]() 、
、![]() ;
;
(iii)若![]() ,则
,则![]() .
.
若所有形如![]() 和
和![]() 的数均不为2014的倍数,则称集合
的数均不为2014的倍数,则称集合![]() 为“好集”.求好集
为“好集”.求好集![]() 所含元素个数的最大值.
所含元素个数的最大值.
【答案】503
【解析】
(1)构造一个503元好集![]() .
.
设![]() .
.
若![]() 、
、![]() 、
、![]() 均不为0,则
均不为0,则
![]() .
.
于是,![]() 为奇数,一定不为2014的倍数.
为奇数,一定不为2014的倍数.
若![]() 、
、![]() 、
、![]() 中有0,不妨设
中有0,不妨设![]() ,则由条件(i)知
,则由条件(i)知![]() 、
、![]() 中至少有一个不为0.
中至少有一个不为0.
由条件(iii)知![]() .
.
注意到,![]() .
.
故![]() 一定不为2014的倍数.
一定不为2014的倍数.
显然,![]() 为奇数,一定不为2014的倍数.
为奇数,一定不为2014的倍数.
则![]() 为503元好集.
为503元好集.
(2)设![]() 为好集.下面证明:
为好集.下面证明:![]() .
.
设![]() 的最小元素为
的最小元素为![]() .则集合
.则集合![]() 中任意两元素的差不为
中任意两元素的差不为![]() .否则,设
.否则,设![]() 、
、![]() ,
,![]() ,得
,得![]() 为2014的倍数,矛盾.
为2014的倍数,矛盾.
将![]() 中大于
中大于![]() 的元素从大到小每
的元素从大到小每![]() 个分为一组,设可分成
个分为一组,设可分成![]() 组,余下的
组,余下的![]() 个数为
个数为![]() ,
,![]() ,…,
,…,![]() .
.
显然,![]() ,
,![]() 组中的每一组至多有
组中的每一组至多有![]() 个数在集合
个数在集合![]() 中.
中.
由好集的定义,知2014、![]() ,且
,且![]() 与
与![]() 不同在集合
不同在集合![]() 中.
中.
不妨设![]() ,否则,只需将集合
,否则,只需将集合![]() 中大于1007的元素换成
中大于1007的元素换成![]() .
.
事实上,若![]() 中有某个
中有某个![]() ,则将其中的
,则将其中的![]() 变为
变为![]() ,将
,将![]() 变为
变为![]() 后得到的数与
后得到的数与![]() 模2014相同.
模2014相同.
下面对![]() 分情形讨论.
分情形讨论.
1)若![]() ,则
,则![]() ,
,![]() ,…,
,…,![]() 中至多有
中至多有![]() 个数属于集合
个数属于集合![]() .
.
故![]()
![]() .
.
2)若![]() ,则
,则![]() .
.
从而,任意一个好集![]() 必满足
必满足![]() .
.
由(1)、(2),知好集![]() 所含元素个数的最大值为503.
所含元素个数的最大值为503.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上![]() 件产品作为样本算出他们的重量(单位:克)重量的分组区间为
件产品作为样本算出他们的重量(单位:克)重量的分组区间为![]() ,
,![]() ,……
,……![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
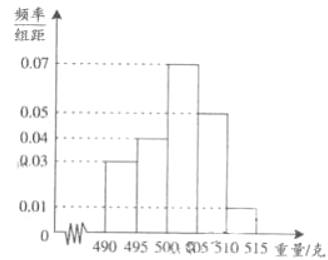
(1)根据频率分布直方图,求重量超过![]() 克的产品数量.
克的产品数量.
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列.
的分布列.
(3)从流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品合格的重量超过
件产品合格的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-x2+a,x∈R,曲线y=f(x)在(0,f(0))处的切线方程为y=bx.
(1)求f(x)的解析式;
(2)当x∈R时,求证:f(x)≥-x2+x;
(3)若f(x)≥kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的某种零件的尺寸![]() 大致服从正态分布
大致服从正态分布![]() ,且规定尺寸
,且规定尺寸![]() 为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
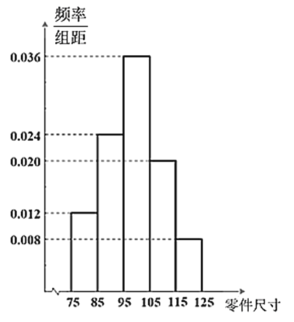
(1)估计生产线生产的零件的次品率及零件的平均尺寸;
(2)从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 个人排成一排,在下列情况下,各有多少种不同排法?
个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,不过原点的直线
,不过原点的直线![]() 与椭圆交于A、B两点.
与椭圆交于A、B两点.
(1)求![]() 面积的最大值.
面积的最大值.
(2)是否存在椭圆![]() ,使得对于椭圆
,使得对于椭圆![]() 的每一条切线与椭圆
的每一条切线与椭圆![]() 均相交,设交于A、B两点,且
均相交,设交于A、B两点,且![]() 恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
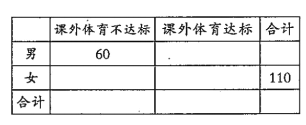
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现按照“课外体育达标”与“课外体育不达标”进行分层抽样,抽取8人,再从这8名学生中随机抽取3人参加体育知识问卷调查,记“课外体育不达标”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

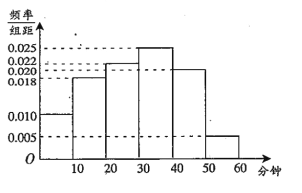
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com