
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,侧棱
底面ABCD,侧棱![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,
,![]() ,
,![]() ,O为AD中点.
,O为AD中点.

(1)求异面直线PB与CD所成角的余弦值;
(2)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中;
(1)BM与ED平行;(2)CN与BE是异面直线;(3)CN与BM所成角为60°;(4)CN与AF垂直. 以上四个命题中,正确命题的序号是( )
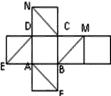
A.(1)(2)(3)B.(2)(4)C.(3)(4)D.(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若直角三角形两直角边长之和为12,求其周长![]() 的最小值;
的最小值;
(2)若三角形有一个内角为![]() ,周长为定值
,周长为定值![]() ,求面积
,求面积![]() 的最大值;
的最大值;
(3)为了研究边长![]() 满足
满足![]() 的三角形其面积是否存在最大值,现有解法如下:
的三角形其面积是否存在最大值,现有解法如下:![]() (其中
(其中![]() , 三角形面积的海伦公式),
, 三角形面积的海伦公式),
∴![]()
![]()
![]()
![]() ,
,
而![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
但是,其中等号成立的条件是![]() ,于是
,于是![]() 与
与![]() 矛盾,
矛盾,
所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的为( )
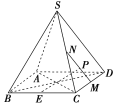
A.①③B.③④C.①②D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=![]() ,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.
,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.

(Ⅰ)证明:平面ADHF⊥平面BCHF;
(Ⅱ)若P为DC的中点,求三棱锥H—AGP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)证明:![]() 为偶函数;
为偶函数;
(2)设![]() ,若对任意的
,若对任意的![]() ,
,![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(3)是否存在正实数![]() ,使得
,使得![]() 在区间
在区间![]() 上的值域刚好是
上的值域刚好是![]() ,若存在,请写在所有满足条件的区间;若不存在,请说明理由.
,若存在,请写在所有满足条件的区间;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足;对任意
,如果满足;对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若![]() 是
是![]() 上的有界函数,且
上的有界函数,且![]() 的上界为3,求实数
的上界为3,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求函数
,求函数![]() 在
在![]() 上的上界
上的上界![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则称
,p为常数),则称![]() 为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
A.![]() 不是等方差数列;
不是等方差数列;
B.若![]() 既是等方差数列,又是等差数列,则该数列为常数列;
既是等方差数列,又是等差数列,则该数列为常数列;
C.已知数列![]() 是等方差数列,则数列
是等方差数列,则数列![]() 是等方差数列;
是等方差数列;
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列.
,k为常数)也是等方差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com