
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为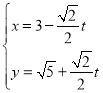 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴,焦距为2,且长轴长是短轴长的
轴,焦距为2,且长轴长是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,过椭圆
,过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,若对满足条件的任意直线
两点,若对满足条件的任意直线![]() ,不等式
,不等式![]() (
(![]() )恒成立,求
)恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有![]() 台大型机器,在
台大型机器,在![]() 个月中,
个月中,![]() 台机器至多出现
台机器至多出现![]() 次故障,且每台机器是否出现故障是相互独立的,出现故障时需
次故障,且每台机器是否出现故障是相互独立的,出现故障时需![]() 名工人进行维修.每台机器出现故障的概率为
名工人进行维修.每台机器出现故障的概率为![]() .已知
.已知![]() 名工人每月只有维修
名工人每月只有维修![]() 台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得
台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得![]() 万元的利润,否则将亏损
万元的利润,否则将亏损![]() 万元.该工厂每月需支付给每名维修工人
万元.该工厂每月需支付给每名维修工人![]() 万元的工资.
万元的工资.
(1)若每台机器在当月不出现故障或出现故障时有工人进行维修,则称工厂能正常运行.若该厂只有![]() 名维修工人,求工厂每月能正常运行的概率;
名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有![]() 名维修工人.
名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘![]() 名维修工人?
名维修工人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图都是由边长为1的正方体叠成的几何体,例如第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位.依此规律,则第![]() 个几何体的表面积是__________个平方单位.
个几何体的表面积是__________个平方单位.
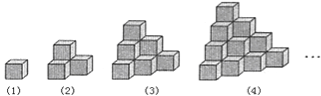
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为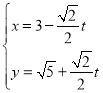 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为![]() .如果
.如果![]() ,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果
,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果![]() ,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为
,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为![]() ,即取出的产品是优质品的概率都为
,即取出的产品是优质品的概率都为![]() ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为![]() (单位:元),求
(单位:元),求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列条件:
,若同时满足下列条件:
①![]() 在
在![]() 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ;
;
那么把![]() 叫闭函数.
叫闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的范围.
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com