
已知函数
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式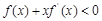 成立, 若
成立, 若 ,
,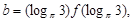
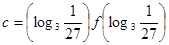 ,则
,则 的大小关系是 .
的大小关系是 .
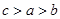
【解析】
试题分析:由已知式子(x)+xf′(x),可以联想到:(uv)′=u′v+uv′,从而可设h(x)=xf(x),有:h′(x)=f(x)+xf′(x)<0,所以利用h(x)的单调性问题很容易解决。解:构造函数h(x)=xf(x),由函数y=f(x)以及函数y=x是R上的奇函数可得h(x)=xf(x)是R上的偶函数,又当x∈(-∞,0)时h′(x)=f(x)+xf′(x)<0,所以函数h(x)在x∈(-∞,0)时的单调性为单调递减函数;所以h(x)在x∈(0,+∞)时的单调性为单调递增函数.又因为函数y=f(x)是定义在R上的奇函数,所以f(0)=0,从而h(0)=0因为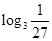 =-3,所以f(
=-3,所以f(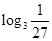 )=f(-3)=-f(3),由0<logπ3<1<50.5<30.5<2,所以h(logπ3)<h(50.5)<h(2)=f(
)=f(-3)=-f(3),由0<logπ3<1<50.5<30.5<2,所以h(logπ3)<h(50.5)<h(2)=f(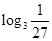 ),即:b<a<c,故答案为.
),即:b<a<c,故答案为.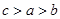
考点:函数奇偶性和单调性
点评:本题考查的考点与方法有:1)所有的基本函数的奇偶性;2)抽象问题具体化的思想方法,构造函数的思想;3)导数的运算法则:(uv)′=u′v+uv′;4)指对数函数的图象;5)奇偶函数在对称区间上的单调性:奇函数在对称区间上的单调性相同;偶函数在对称区间上的单调性相反;5)奇偶函数的性质:奇×奇=偶;偶×偶=偶;奇×偶=奇(同号得正、异号得负);奇+奇=奇;偶+偶=偶.本题结合已知构造出h(x)是正确解答的关键所在


科目:高中数学 来源:2012-2013学年浙江省绍兴一中高二下学期期中考试理科数学试卷(带解析) 题型:填空题
已知函数
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是 .
的大小关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com