
如图1,在正方形 中,点
中,点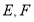 分别是
分别是 的中点,
的中点, 与
与 交于点
交于点 为
为 中点,点
中点,点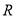 在线段
在线段 上,且
上,且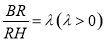 .现将
.现将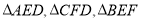 分别沿
分别沿 折起,使点
折起,使点 重合于点
重合于点 (该点记为
(该点记为 ),如图2所示.
),如图2所示.

(1)若 ,求证:
,求证: 平面
平面 ;
;
(2)是否存在正实数 ,使得直线
,使得直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源:2017届江苏南京市盐城高三一模考试数学试卷(解析版) 题型:解答题
如图所示,某街道居委会拟在 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段 上建一个活动中心,其中
上建一个活动中心,其中 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形 ,上部分是以
,上部分是以 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长 不超过
不超过 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角 满足
满足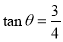 .
.

(1)若设计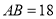 米,
米, 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计 与
与 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中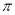 取3)
取3)
查看答案和解析>>
科目:高中数学 来源:2017届四川成都市高三理一诊考试数学试卷(解析版) 题型:填空题
我国南北朝时期的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”。“势”即是高,“幂”是面积。意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等。类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为1的梯形,且当实数 取
取 上的任意值时,直线
上的任意值时,直线 被图1和图2所截得的两线段长始终相等,则图1的面积为 ___________.
被图1和图2所截得的两线段长始终相等,则图1的面积为 ___________.

查看答案和解析>>
科目:高中数学 来源:2017届四川成都市高三理一诊考试数学试卷(解析版) 题型:选择题
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为( )

A.  B.
B. 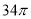 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届广西柳州市高三文10月模拟考试数学试卷(解析版) 题型:解答题
中国柳州从2011年起每年国庆期间都举办一届国际水上狂欢节,到2016年已举办了六届,旅游部门统计在每届水上狂欢节期间,吸引了不少外地游客到柳州,这将极大地推进柳州的旅游业的发展,现将前五届水上狂欢节期间外地游客到柳州的人数统计如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
水上狂欢节届编号 | 1 | 2 | 3 | 4 | 5 |
外地游客人数 | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
(1)求 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)利用(1)中的线性回归方程,预测2017年第7届柳州国际水上狂欢节期间外地游客到柳州的人数.
参考公式: ,
, .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com