
【题目】已知![]() 是定义在
是定义在![]() 上的函数,满足
上的函数,满足 .
.
(1)证明:2是函数![]() 的周期;
的周期;
(2)当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 时的解析式,并写出
时的解析式,并写出![]() 在
在![]() (
(![]() )时的解析式;
)时的解析式;
(3)对于(2)中的函数![]() ,若关于x的方程
,若关于x的方程![]() 恰好有20个解,求实数a的取值范围.
恰好有20个解,求实数a的取值范围.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,如果对于定义域
,如果对于定义域![]() 内的任意实数
内的任意实数![]() ,对于给定的非零常数
,对于给定的非零常数![]() ,总存在非零常数
,总存在非零常数![]() ,恒有
,恒有![]() 成立,则称函数
成立,则称函数![]() 是
是![]() 上的
上的![]() 级类增周期函数,周期为
级类增周期函数,周期为![]() ,若恒有
,若恒有![]() 成立,则称函数
成立,则称函数![]() 是
是![]() 上的
上的![]() 级类周期函数,周期为
级类周期函数,周期为![]() .
.
(1)已知函数![]() 是
是![]() 上的周期为1的2级类增周期函数,求实数
上的周期为1的2级类增周期函数,求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,
,![]() 是
是![]() 上的
上的![]() 级类周期函数,且
级类周期函数,且![]() 是
是![]() 上的单调增函数,当
上的单调增函数,当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是底面边长为
是底面边长为![]() 的正四棱柱,
的正四棱柱,![]() 是
是![]() 和
和![]() 的交点.
的交点.
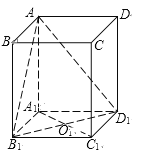
(1)若正四棱柱的高与底面边长相等,求二面角![]() 的大小(结果用反三角函数值表示);
的大小(结果用反三角函数值表示);
(2)若点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求正四棱柱
,求正四棱柱![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点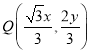 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆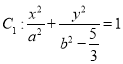 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 经过曲线
经过曲线![]() 的焦点
的焦点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com