
【题目】已知抛物线![]() :
:![]() 上任意一点到其焦点的距离的最小值为1.
上任意一点到其焦点的距离的最小值为1.![]() ,
,![]() 为抛物线上的两动点(
为抛物线上的两动点(![]() 、
、![]() 不重合且均异于原点),
不重合且均异于原点),![]() 为坐标原点,直线
为坐标原点,直线![]() 、
、![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() .
.
(1)求抛物线方程;
(2)若![]() ,求证直线
,求证直线![]() 过定点;
过定点;
(3)若![]() (
(![]() 为定值),探求直线
为定值),探求直线![]() 是否过定点,并说明理由.
是否过定点,并说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)是,理由见解析.
;(2)证明见解析;(3)是,理由见解析.
【解析】
(1)根据抛物线的定义结合已知求出![]() 的值,最后写出抛物线的标准方程;
的值,最后写出抛物线的标准方程;
(2)设出直线![]() 的方程与抛物线方程联立,由已知
的方程与抛物线方程联立,由已知![]() 可以得到
可以得到![]() ,结合平面向量数量积坐标运算公式、一元二次方程根与系数关系,最后得到直线
,结合平面向量数量积坐标运算公式、一元二次方程根与系数关系,最后得到直线![]() 过定点;
过定点;
(3)根据(2)中的特例,再结合![]() ,根据两角和的正切公式、直线倾斜角和斜率的关系,最后能求出直线
,根据两角和的正切公式、直线倾斜角和斜率的关系,最后能求出直线![]() 所过定点.
所过定点.
(1)设![]() 为抛物线上任一点,
为抛物线上任一点,![]() 为焦点,则
为焦点,则![]() ,
,
故抛物线方程![]() .
.
(2)设![]() ,
,![]() ,
,![]() :
:![]() ,联立
,联立![]() 得
得![]() ,
,
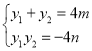 ,
,
![]() ,即
,即![]() ,
,
则![]()
![]() .
.
得已![]() ,从而直线
,从而直线![]() 过定点
过定点![]() .
.
(3)由(2),![]() :
:![]() ,
,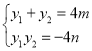 ,
,
当![]() 或
或![]() 时,
时,![]() ,
,
![]() ,故
,故![]() ,
,
于是直线![]() 经过定点
经过定点![]() .
.
当![]() 且
且![]() 时,
时,![]() ,
,
![]()
![]() ,
,
即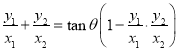
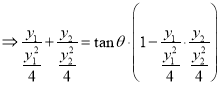 ,
,
![]()
![]()
![]() .
.
故直线![]() :
:![]() ,即为
,即为![]() ,
,
故直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线C:y2=8x上一点A到焦点F的距离为6,若点P为抛物线C准线上的动点,则|OP|+|AP|的最小值为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .我们将其结论推广:椭圆
.我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用.已知,直线
,在解本题时可以直接应用.已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求![]() 的值
的值
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .当
.当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com