
【题目】已知函数f(x)=ex﹣ax
(1)讨论函数f(x)的单调性;
(2)若存在x1<x2,且满足f(x1)=(x2).证明![]() ;
;
(3)证明:![]() (n∈N).
(n∈N).
【答案】(1)见解析(2)见解析(3)见解析
【解析】
(1)求出![]() ,对
,对![]() 分类讨论,求出
分类讨论,求出![]() 的解,即可得出结论;
的解,即可得出结论;
(2)由(1)可得a>0,且x1<lna<x2,问题转化为证明![]() ,等价于证明
,等价于证明![]() ,即证
,即证![]() ,即证f(x2)>f(2lna﹣x2),
,即证f(x2)>f(2lna﹣x2),
构造函数h(x)=f(x)﹣f(2lna﹣x),x∈(lna,+∞),即可证明结论;
(3)对比证明不等式与![]() 的解析式关系,令
的解析式关系,令![]() ,令
,令![]() ,将不等式左式放缩为等比数列的和,即可证明结论.
,将不等式左式放缩为等比数列的和,即可证明结论.
(1)f′(x)=ex﹣a,
当a≤0时,f′(x)>0,f(x)在(﹣∞,+∞)上递增,
当a>0时,x>lna时,f′(x)>0,f(x)在(lna,+∞)上递增,
x<lna时,f′(x)<0,f(x)在(﹣∞,lna)上递减;
(2)由(1)知,a>0,且x1<lna<x2,
记h(x)=f(x)﹣f(2lna﹣x),x∈(lna,+∞),
则h′(x)![]() 2+(a﹣1)2﹣1>0,
2+(a﹣1)2﹣1>0,
所以h(x)在(lna,+∞)上递增,则h(x)>h(lna)=0,
所以f(x)>f(2lna﹣x),则f(x2)>f(2lna﹣x2),
因为f(x2)=f(x1),f(x1)>f(2lna﹣x2),
![]() ,
,
![]() ,所以
,所以![]() ;
;
(3)由(1)可知a=e时,f(x)≥f(lne)=0,
所以ex≥ex,所以ex﹣1≥x,当且仅当x=1时取等号,
令x=2n(n∈N),![]() ,当n=0时取等号,
,当n=0时取等号,
则![]() (n∈N).
(n∈N).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示.
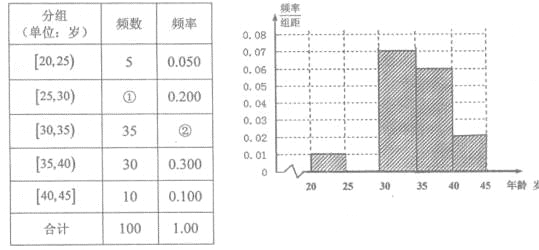
(Ⅰ)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且a3+2S6=77,a10﹣a5=10.
(1)求数列{an}的通项公式;
(2)数列{bn}满足:b1=1,bn﹣bn﹣1=an﹣n+1(n≥2),求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为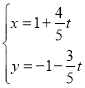 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=cosθ﹣sinθ.
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=cosθ﹣sinθ.
(1)求直线l被曲线C所截得的弦长;
(2)若M(x,y)是曲线C上的动点,求x+y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 均为各项都不相等的数列,
均为各项都不相等的数列,![]() 为
为![]() 的前n项和,
的前n项和,![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 是公比为
是公比为![]() 的等比数列,求证:数列
的等比数列,求证:数列![]() 为等比数列;
为等比数列;
![]() 若
若![]() 的各项都不为零,
的各项都不为零,![]() 是公差为d的等差数列,求证:
是公差为d的等差数列,求证:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列的充要条件是
成等差数列的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(1)求椭圆的方程;
(2)直线l:y=kx+m与椭圆交于点A,C,线段AC的中点为M,射线MO与椭圆交于点P,点O为△PAC的重心,求证:△PAC的面积S为定值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=a(|sinx|+|cosx|)﹣sin2x﹣1,a∈R.
(1)写出函数 f(x)的最小正周期(不必写出过程);
(2)求函数 f(x)的最大值;
(3)当a=1时,若函数 f(x)在区间(0,kπ)(k∈N*)上恰有2015个零点,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
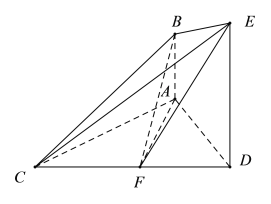
(1)求证:面BCE⊥面DCE;
(2)求二面角C﹣BE﹣F的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com