分析:(Ⅰ)由l与圆相切,知m
2=1+k
2,由
,得(1-k
2)x
2-2mkx-(m
2+1)=0,故k的取值范围为(-1,1).由此能求出x
2-x
1取最小值
2.
(Ⅱ)由已知可得A
1,A
2的坐标分别为(-1,0),(1,0),所以
k1•k2==
| (kx1+m)(kx2+m) |
| (x1+1)(x2-1) |
=
,由此能求出
k1•k2==-(3+2)为定值.
解答:解:(Ⅰ)∵l与圆相切,
∴
1=,
∴m
2=1+k
2①
由
,
得(1-k
2)x
2-2mkx-(m
2+1)=0,
∴
| | 1-k2≠0 | | △=4m2k2+4(1-k2) | | x1•x2=<0 |
| |
(m2+1)=4(m2+1-k2)=8>0,
∴k
2<1,
∴-1<k<1,
故k的取值范围为(-1,1).
由于
x1+x2=∴x2-x1===,
∵0≤k
2<1
∴当k
2=0时,x
2-x
1取最小值
2.(6分)
(Ⅱ)由已知可得A
1,A
2的坐标分别为(-1,0),(1,0),
∴
k1=,k2=,
∴
k1•k2==
| (kx1+m)(kx2+m) |
| (x1+1)(x2-1) |
=
| k2x1x2+mk(x1+x2)+m2 |
| x1x2+(x2-x1)-1 |
=
=
| m2k2+k2-2m2k2+m2k2-m2 |
| m2+1-2-k2+1 |
=
,
由①,得m
2-k
2=1,
∴
k1•k2==-(3+2)为定值.(12分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

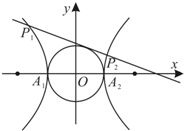 已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).
已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案