
(Ⅰ)求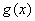 ;
;
(Ⅱ)当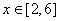 时,恒有
时,恒有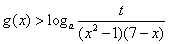 成立,求t的取值范围;
成立,求t的取值范围;
(Ⅲ)当0<a≤时,试比较f(1)+f(2)+…+f(n)与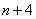 的大小,并说明理由.
的大小,并说明理由.
解:(1)由题意得:ax=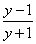 >0
>0
故g(x)=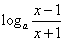 ,x∈(-∞,-1)∪(1,+∞)……………………3分
,x∈(-∞,-1)∪(1,+∞)……………………3分
(2) 由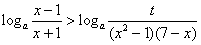 得
得
①当a>1时,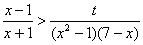 >0
>0
又因为x∈[2,6],所以0<t<(x-1)2(7-x)
令h(x)=(x-1)2(7-x)=-x3+9xx+7, x∈[2,6]
则h'(x)=-3x2+18x-15=-3(x-1)(x-5)
列表如下:
|
x |
2 |
(2,5) |
5 |
(5,6) |
6 |
|
h'(x) |
|
+ |
0 |
- |
|
|
h(x) |
5 |
↗ |
极大值32 |
↘ |
25 |
所以h(x)最小值=5,
所以0<t<5
②当0<a<1时,0<
又因为x∈[2,6],所以t>(x-1)2(7-x)>0
令h(x)=(x-1)2(7-x)=-x3+9xx+7, x∈[2,6]
由①知h(x)最大值=32, x∈[2,6]
所以t>32
综上,当a>1时,0<t<5;当0<a<1时,t>32.……………………9分
(3)设a=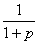 ,则p≥1
,则p≥1
当n=1时,f(1)=1+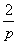 ≤3<5
≤3<5
当n≥2时
设k≥2,k∈N *时
则f(k)=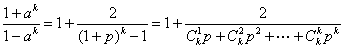
所以f(k)≤1+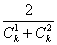 =1+
=1+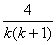 =1+
=1+
从而f(2)+f(3)+……+f(n)≤n-1+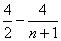 <n+1
<n+1
所以f(1)+f(2)+f(3)+……+f(n)<f(1)+n+1≤n+4
综上,总有f(1)+f(2)+f(3)+……+f(n)<n+4……………………14分


科目:高中数学 来源: 题型:
| aj | ai |
查看答案和解析>>
科目:高中数学 来源: 题型:
| θ |
| 2 |
| θ |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| π |
| 3 |
| 7π |
| 12 |
| a |
| b |
| 1 |
| 2 |
| 4 |
| 5 |
| 5π |
| 12 |
| 13π |
| 12 |
| a |
| b |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com