
【题目】某国际性会议纪念章的一特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向该会议的组织委员会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时,该店一年可销售2000枚,经过市场调研发现,每枚纪念章的销售价格在每枚20元的基础上,每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元(每枚的销售价格应为正整数).
元(每枚的销售价格应为正整数).
(1)写出该特许专营店一年内销售这种纪念章所获得的利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() 的函数关系式;
的函数关系式;
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出这个最大值;
(元)最大,并求出这个最大值;
科目:高中数学 来源: 题型:
【题目】 设函数![]()
(1)如果![]() ,那么实数
,那么实数![]() ___;
___;
(2)如果函数![]() 有且仅有两个零点,那么实数
有且仅有两个零点,那么实数![]() 的取值范围是___.
的取值范围是___.
【答案】![]() 或4;
或4;![]()
【解析】
试题分析:由题意![]() ,解得
,解得![]() 或
或![]() ;
;
第二问如图:
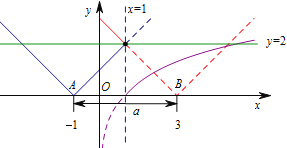
![]() 的图象是由两条以
的图象是由两条以![]() 为顶点的射线组成,当
为顶点的射线组成,当![]() 在A,B 之间(包括
在A,B 之间(包括![]() 不包括
不包括![]() )时,函数
)时,函数![]() 和
和![]() 有两个交点,即
有两个交点,即![]() 有两个零点.所以
有两个零点.所以![]() 的取值范围为
的取值范围为![]() .
.
考点:1.分段函数值;2.函数的零点.
【题型】填空题
【结束】
15
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
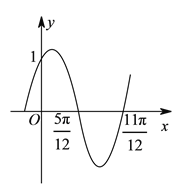
(![]() )求函数
)求函数![]() 的解析式.
的解析式.
(![]() )求函数
)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由;
的范围(或值),若不存在,请说明理由;
(3)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值,并写出
的值,并写出![]() 在区间
在区间![]() 上的增减性和值域(不需要证明);
上的增减性和值域(不需要证明);
(2)令![]() ,其中
,其中![]() ,若
,若![]() 对任意
对任意![]() 、
、![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)令![]() ,若
,若![]() 对任意
对任意![]() 、
、![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时,某地上班族![]() 中的成员仅以自驾或公交方式通勤,分析显示:当
中的成员仅以自驾或公交方式通勤,分析显示:当![]() 中
中![]() 的成员自驾时,自驾群体的人均通勤时间为
的成员自驾时,自驾群体的人均通勤时间为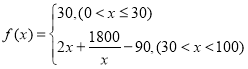 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;并求
的表达式;并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件![]() “取出的两球同色”,
“取出的两球同色”,![]() “取出的2球中至少有一个黄球”,
“取出的2球中至少有一个黄球”,![]() “取出的2球至少有一个白球”,
“取出的2球至少有一个白球”,![]() “取出的两球不同色”,
“取出的两球不同色”,![]() “取出的2球中至多有一个白球”.下列判断中正确的序号为________.
“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①![]() 与
与![]() 为对立事件;②
为对立事件;②![]() 与
与![]() 是互斥事件;③
是互斥事件;③![]() 与
与![]() 是对立事件:④
是对立事件:④![]() ;⑤
;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 时,
时,![]() 的值为2千克/年;当
的值为2千克/年;当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 时,因缺氧等原因,
时,因缺氧等原因,![]() 的值为0千克/年.
的值为0千克/年.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当养殖密度![]() 为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,且AB![]() BP
BP![]() 2,AD=AE=1,AE⊥AB,且AE∥BP.
2,AD=AE=1,AE⊥AB,且AE∥BP.

(1)求平面PCD与平面ABPE所成的二面角的余弦值;
(2)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com