
【题目】某商场为了吸引大家,规定:购买一定价值的商品可以获得一张奖券,奖券上有一个兑奖号码,可以分别参加两次抽奖方式相同的兑奖活动,已知甲有一张该商场的奖券,且每次兑奖活动的中奖概率都是0.05,求:
(1)甲中两次奖的概率;
(2)甲中一次奖的概率;
(3)甲不中奖的概率.
【答案】(1)0.0025;(2)0.095;(3)0.9025
【解析】
(1)“甲中两次奖”为事件![]() ,
,![]() 相互独立,根据相互独立事件的概率求法即可求解.
相互独立,根据相互独立事件的概率求法即可求解.
(2)“甲中一次奖”为事件![]() ,
,![]() 与
与![]() 互斥且
互斥且![]() 相互独立,根据相互独立事件的概率乘法以及互斥事件满足概率的加法即可求解.
相互独立,根据相互独立事件的概率乘法以及互斥事件满足概率的加法即可求解.
(3)“甲不中奖”为事件![]() ,
,![]() 相互独立,根据相互独立事件的概率求法即可求解.
相互独立,根据相互独立事件的概率求法即可求解.
解:设事件![]() 为“甲第
为“甲第![]() 次中奖”,则
次中奖”,则![]() .
.
(1)“甲中两次奖”为事件![]() ,因为
,因为![]() 相互独立,所以
相互独立,所以![]() ,即甲中两次的概率为0.0025.
,即甲中两次的概率为0.0025.
(2)“甲中一次奖”为事件![]() ,由于
,由于![]() 与
与![]() 互斥且
互斥且![]() 相互独立,所以:
相互独立,所以:![]()
![]() ,即甲中一次奖的概率为0.095.
,即甲中一次奖的概率为0.095.
(3)“甲不中奖”为事件![]() ,由于
,由于![]() 相互独立,所以
相互独立,所以![]() ,即甲不中奖的概率为0.9025
,即甲不中奖的概率为0.9025


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
B.若三个平面两两相交,其中两个平面的交线与第三个平面平行.则另外两条交线平行;
C.如果![]() 是两条异面直线,那么直线
是两条异面直线,那么直线![]() 一定是异面直线;
一定是异面直线;
D.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 绕
绕![]() 所在直线旋转一周,所形成的几何体的轴截面面积为10.
所在直线旋转一周,所形成的几何体的轴截面面积为10.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为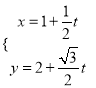 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
⑴ 求证:数列![]() 为等差数列;
为等差数列;
⑵ 设![]() ,
, ![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若当
,若当![]() 且
且![]() 为偶数时,
为偶数时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,试求数列
,试求数列![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意
,若对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 具有性质P.
具有性质P.
(1)若数列![]() 是首项为1,公比为2的等比数列,试判断数列
是首项为1,公比为2的等比数列,试判断数列![]() 是否具有性质P;
是否具有性质P;
(2)若正项等差数列![]() 具有性质P,求数列
具有性质P,求数列![]() 的公差;
的公差;
(3)已知正项数列![]() 具有性质P,
具有性质P,![]() ,且对任意
,且对任意![]() ,有
,有![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 图象上最高点与该最高点相邻的图象的对称中心的距离为
图象上最高点与该最高点相邻的图象的对称中心的距离为![]() .
.
(1)求函数![]() 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)把![]() 图象上所有的点先横坐标伸长为原来的
图象上所有的点先横坐标伸长为原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位得到函数
个单位得到函数![]() 的图象.在
的图象.在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别是角
分别是角![]() ,
, ![]() ,
, ![]() 的对边,若
的对边,若![]() ,
, ![]() 的面积为
的面积为![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,求
成等差数列,求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com