
【题目】已知四棱锥![]() ,底面ABCD是边长为1的正方形,
,底面ABCD是边长为1的正方形,![]() ,平面
,平面![]() 平面ABCD,当点C到平面ABE的距离最大时,该四棱锥的体积为( )
平面ABCD,当点C到平面ABE的距离最大时,该四棱锥的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)如图,在直角坐标系![]() 中,角
中,角![]() 的顶点是原点,始边与
的顶点是原点,始边与![]() 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点![]() ,且
,且![]() ,将角
,将角![]() 的终边按逆时针方向旋转
的终边按逆时针方向旋转![]() ,交单位圆于点
,交单位圆于点![]() ,记
,记![]() .
.
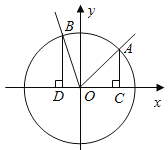
(1)若![]() ,求
,求![]() ;
;
(2)分别过![]() 作
作![]() 轴的垂线,垂足依次为
轴的垂线,垂足依次为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数且
为参数且 ![]() )曲线
)曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点到极点的距离;
的交点到极点的距离;
(2)设![]() 与
与![]() 交于
交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 点,当
点,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() a(x﹣1)2+(x﹣2)ex(a>0).
a(x﹣1)2+(x﹣2)ex(a>0).
(1)讨论函数f(x)的单调性;
(2)若关于x的方程f(x)![]() a=0存在3个不相等的实数根,求实数a的取值范围.
a=0存在3个不相等的实数根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系xOy的原点为极坐标系的极点,x轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,P是
,P是![]() 上一动点,
上一动点,![]() ,Q的轨迹为
,Q的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程,
的极坐标方程,并化为直角坐标方程,
(2)若点![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与曲线
(t为参数),直线l与曲线![]() 的交点为A,B,当
的交点为A,B,当![]() 取最小值时,求直线l的普通方程.
取最小值时,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有![]() 或者
或者![]() 两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为![]() ,记抽到的废品数为
,记抽到的废品数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为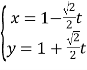 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com