
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)过点
(a>b>0)过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
(2)若斜率为![]() 的直线l与椭圆C交于A,B两点,试探究
的直线l与椭圆C交于A,B两点,试探究![]() 是否为定值?若是定值,则求出此定值;若不是定值,请说明理由.
是否为定值?若是定值,则求出此定值;若不是定值,请说明理由.
【答案】(1)![]() (2)是定值,7
(2)是定值,7
【解析】
(1)由离心率的值可设椭圆C的方程为![]() ,代入点
,代入点![]() 的坐标即可求得c,从而求得椭圆方程;(2)设直线l的方程为y=
的坐标即可求得c,从而求得椭圆方程;(2)设直线l的方程为y=![]() x+n,A(x1,y1),B(x2,y2),用x1、x2表示OA2+OB2,联立直线方程与椭圆方程得到关于x的一元二次方程,韦达定理求出
x+n,A(x1,y1),B(x2,y2),用x1、x2表示OA2+OB2,联立直线方程与椭圆方程得到关于x的一元二次方程,韦达定理求出![]() 、
、![]() ,代入
,代入![]() 即可得解.
即可得解.
(1)由离心率![]() ,得a∶b∶c=2∶
,得a∶b∶c=2∶![]() ∶1,
∶1,
则可设椭圆C的方程为![]() ,
,
由点![]() 在椭圆C上,得
在椭圆C上,得![]() ,即c2=1,
,即c2=1,
所以椭圆C的方程为![]()
(2)设直线l的方程为y=![]() x+n,A(x1,y1),B(x2,y2),
x+n,A(x1,y1),B(x2,y2),
所以OA2+OB2=![]() +3-
+3-![]()
![]() +
+![]() +3-
+3-![]() =
=![]() (
(![]() +
+![]() )+6.
)+6.
由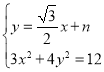 消去y得3x2+2
消去y得3x2+2![]() nx+2n2-6=0.
nx+2n2-6=0.
当Δ>0时,x1+x2=-![]() n,x1x2=
n,x1x2=![]() ,
,
从而![]() =4,
=4,
所以OA2+OB2=7,为定值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ+ρsinθ=1,曲线C的极坐标方程为ρsin2θ=8cosθ.
(1)求直线l与曲线C的直角坐标方程;
(2)设点M(0,1),直线l与曲线C交于不同的两点P,Q,求|MP|+|MQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年世界海洋日暨全国海洋宣传日主场活动在海南三亚举行,此次活动主题为“珍惜海洋资源保护海洋生物多样性”,旨在进一步提高公众对节约利用海洋资源.保护海洋生物多样性的认识,为保护蓝色家园做出贡献.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”,为了响应世界海洋日的活动,2019年12月北京某高校行政主管部门从该大学随机抽取部分大学生进行一次海洋知识测试,并根据被测验学生的成绩(得分都在区间![]() 内)绘制成如图所示的频率分布直方图.
内)绘制成如图所示的频率分布直方图.
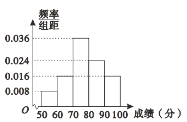
若学生的得分成绩不低于80分的认为是“成绩优秀”现在从认为“成绩优秀”的学生中根据原有分组按照分层抽样的方法抽取10人进行奖励,最后再从这10人中随机选取3人作为优秀代表发言.
(1)求所抽取的3人不属于同一组的概率;
(2)记这3人中,![]() 为测试成绩在
为测试成绩在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足
的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足![]() .过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N,则
.过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,定义:
,定义:![]() 表示不超过
表示不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() .
.
(1)若![]() ,写出实数
,写出实数![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,若对于任意的
,若对于任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com