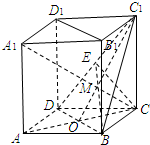
解:(Ⅰ)∵B
1D
1∥BD,
又BD?平面C
1BD,B
1D
1?平面C
1BD,∴B
1D
1∥平面C
1BD.…(2分)
(Ⅱ)连接AC,交BD于O,则BD⊥AC.
又A
1A⊥BD,∴BD⊥平面A
1AC.∵A
1C?平面A
1AC,BD⊥A
1C.
连接C
1O,在矩形A
1C
1CA中,设A
1C交C
1O于M.
由
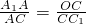
,知∠ACA
1=∠CC
1O.∴
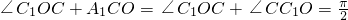
,∴
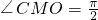
,∴A
1C⊥C
1O.
又CO∩BD=0,CO?平面C
1BD,BD?平面C
1BD,∴A
1C⊥平面C
1BD.…(7分)
(Ⅲ)取DC
1的中点E,连接BE,CD.
∵BD=BC
1,∴BE⊥DC
1.∵CD=CC
1,∴CE⊥DC
1.∠BEC为二面角B-C
1D-C的平面角.
设正方体的棱长为a,则
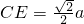
.
又由
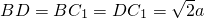
,得
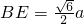
.
在△BEC中,由余弦定理,得
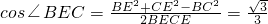
.
所以所求二面角的余弦值为

.…(12分)
分析:(I)根据正方体的几何特征可得B
1D
1∥BD,结合线面平行的判定定理,即可得到B
1D
1∥平面C
1BD;
(Ⅱ)连接AC,交BD于O,则BD⊥AC,结合A
1A⊥BD,由线面垂直的判定定理得BD⊥平面A
1AC,进而BD⊥A
1C,连接C
1O,可证得A
1C⊥C
1O,再利用线面垂直的判定定理即可得到A
1C⊥平面C
1BD;
(Ⅲ)取DC
1的中点E,连接BE,CD.根据二面角的定义,可判断出∠BEC为二面角B-C
1D-C的平面角,解△BEC即可求出二面角B-C
1D-C的余弦值.
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,其中(I)的关键是根据正方体的几何特征得B
1D
1∥BD,(II)的关键是得到BD⊥A
1C,A
1C⊥C
1O,(III)的关键是确定∠BEC为二面角B-C
1D-C的平面角.

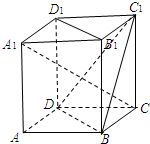 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中, 解:(Ⅰ)∵B1D1∥BD,
解:(Ⅰ)∵B1D1∥BD,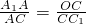 ,知∠ACA1=∠CC1O.∴
,知∠ACA1=∠CC1O.∴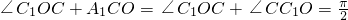 ,∴
,∴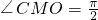 ,∴A1C⊥C1O.
,∴A1C⊥C1O.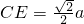 .
.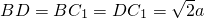 ,得
,得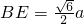 .
.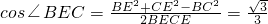 .
. .…(12分)
.…(12分)

 阅读快车系列答案
阅读快车系列答案 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则