
(本题满分12分)通常情况下,同一地区一天的温度随时间变化的曲线接近于函数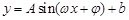 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为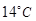 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下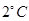 .
.
(Ⅰ)请推理荆门地区该时段的温度函数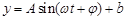
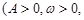
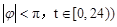 的表达式;
的表达式;
(Ⅱ)29日上午9时某高中将举行期末考试,如果温度低于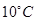 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2014届云南省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)等比数列 中,已知
中,已知 。(1)求数列
。(1)求数列 的通项公式;(2)已知数列
的通项公式;(2)已知数列 是等差数列,且
是等差数列,且 和
和 的第2项、第4项分别相等。若数列
的第2项、第4项分别相等。若数列 的前
的前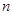 项和
项和 ,求
,求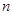 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014届吉林松原扶余县第一中学高二第一次月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知数列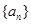 的前
的前 项和为
项和为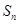 ,
, (
(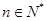 ).
).
(Ⅰ)证明数列 是等比数列,求出数列
是等比数列,求出数列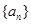 的通项公式;
的通项公式;
(Ⅱ)设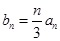 ,求数列
,求数列 的前
的前 项和
项和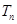 ;
;
(Ⅲ)数列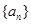 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届吉林长春外国语学校高二下期中理科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知数列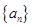 的前
的前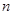 和为
和为 ,其中
,其中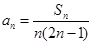 且
且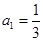
(1)求
(2)猜想数列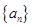 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省泉州四校高三第二次联考考试文科数学 题型:解答题
(本题满分12分)等比数列 中,已知
中,已知
1)求数列 的通项
的通项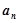
2)若等差数列 ,
, ,求数列
,求数列 前n项和
前n项和 ,并求
,并求 最大值
最大值
|
|
第一批 |
第二批 |
第三批 |
|
北京 |
200 |
|
|
|
香港 |
150 |
160 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com