
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:

(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【答案】(1)见解析;(2)![]() .(2)质量提升月”活动后的质量指标值的均值比活动前大约提升了
.(2)质量提升月”活动后的质量指标值的均值比活动前大约提升了![]() .
.
【解析】试题分析:(1)根据频率分布直方图,一、二等品所占比例的估计值为
![]() ,可做出判断.
,可做出判断.
(2)由频率分布直方图的频率分布可知8件产品中,一等品3件,二等品4件,三等品1件,分类讨论各种情况可得![]() .
.
(3)算出“质量提升月”活动前,后产品质量指标值为![]() ,可得质量指标值的均值比活动前大约提升了17.6
,可得质量指标值的均值比活动前大约提升了17.6
试题解析:(1)根据抽样调查数据,一、二等品所占比例的估计值为![]() ,由于该估计值小于0.92,故不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定.
,由于该估计值小于0.92,故不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定.
(2)由频率分布直方图知,一、二、三等品的频率分别为0.375、0.5、0.125,故在样本中用分层抽样方法抽取的8件产品中,一等品3件,二等品4件,三等品1件,再从这8件产品中随机抽取4件,一、二、三等品都有的情况有2种:①一等品2件,二等品1件,三等品1件;②一等品1件,二等品2件,三等品1件,故所求的概率![]() .
.
(3)“质量提升月”活动前,该企业这种产品的质量指标值的均值约为
![]()
![]()
“质量提升月”活动后,产品质量指标值![]() 近似满足
近似满足![]() ,则
,则![]() .
.
所以,“质量提升月”活动后的质量指标值的均值比活动前大约提升了17.6


科目:高中数学 来源: 题型:
【题目】(导学号:05856332)
已知三棱柱ABC-A1B1C1如图所示,其中CA⊥平面ABB1A1,四边形ABB1A1为菱形,∠AA1B1=60°,E为BB1的中点,F为CB1的中点.
(Ⅰ)证明:平面AEF⊥平面CAA1C1;
(Ⅱ)若CA=2,AA1=4,求B1到平面AEF的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标准温度和大气压下,人体血液中氢离子的物质的量的浓度(单位mol/L,记作![]() )和氢氧根离子的物质的量的浓度(单位mol/L,记作
)和氢氧根离子的物质的量的浓度(单位mol/L,记作![]() )的乘积等于常数
)的乘积等于常数![]() .已知pH值的定义为
.已知pH值的定义为![]() ,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的
,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的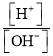 可以为(参考数据:
可以为(参考数据: ![]() ,
, ![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+1)=-f(x),且当x∈[0,1)时,f(x)=log2(x+1),给出下列命题
①f(2014)+f(-2015)=0;
②函数f(x)在定义域上是周期为2的函数;
③直线y=x与函数f(x)的图象有2个交点;
④函数f(x)的值域为(-1,1).
其中正确的是( )
A. ①② B. ②③
C. ①④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若圆心在曲线![]() 上的动圆
上的动圆![]() 过点
过点![]() ,试证明圆
,试证明圆![]() 与
与![]() 轴必相交,且截
轴必相交,且截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.
(1)求抛物线的方程;
(2)过F的直线l与抛物线相交于A,D两点,与圆![]() 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.

根据表中数据估计,该校4000名学生中约有120名这4次活动均未参加.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从该校4000名学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅲ)已知学生每次参加公益活动可获得10个公益积分,任取该校一名学生,记该生2017年12月获得的公益积分为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[1,+∞)上的函数f(x)满足:①f(2x)=2f(x);②当2≤x≤4时,f(x)=1-|x-3|.则函数g(x)=f(x)-2在区间[1,28]上的零点个数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com