
分析 (1)求出f′(x),由f'(3)=0,求解得到a的值即可;
(2)因为函数在(-∞,0)上为增函数令f'(x)=0得到函数的驻点,由a的取值范围研究函数的增减性得到函数为增函数时a的范围即可.
解答 解:(1)f'(x)=6x2-6(a+1)x+6a=6(x-a)(x-1).
因f'(3)=6(3-a)(3-1)=0.解得a=3.
(2)令f'(x)=6(x-a)(x-1)=0得x1=a,x2=1.
当a<1时,若x∈(-∞,a)∪(1,+∞),则f'(x)>0,
所以f(x)在(-∞,a)和(1,+∞)上为增
函数,故当0≤a<1时,f(x)在(-∞,0)上为增函数.
当a≥1时,若x∈(-∞,1)∪(a,+∞),则f'(x)>0,
所以f(x)在(-∞,1)和(a,+∞)上为增函
数,从而f(x)在(-∞,0]上也为增函数.
综上所述,当a∈[0,+∞)时,f(x)在(-∞,0)上为增函数.
点评 考查学生利用导数研究函数极值及单调性的运用能力.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 任一事件的概率总在(0,1)内 | B. | 不可能事件的概率不一定为0 | ||
| C. | 必然事件的概率一定为1 | D. | 概率为0的事件一定是不可能事件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①②③ | C. | ①② | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | ±$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
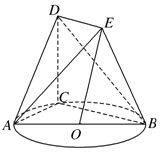 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com