
(本小题满分14分)
已知函数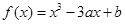 在
在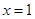 处有极小值
处有极小值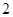 。
。
(1)求函数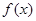 的解析式;
的解析式;
(2)若函数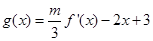 在
在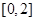 只有一个零点,求
只有一个零点,求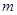 的取值范围。
的取值范围。
(1) (2)
(2) ,或
,或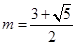 ,或
,或
解析试题分析:(1) 1分
1分
依题意有 , 3分
, 3分
解得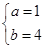 , 4分
, 4分
此时 ,
,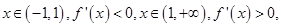 满足
满足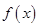 在
在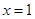 处取极小值
处取极小值
∴ 5分
5分
(2)
∴ …………6分
…………6分
当 时,
时,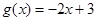 ,∴
,∴ 在
在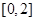 上有一个零点
上有一个零点 (符合),……8分
(符合),……8分
当 时,
时,
①若方程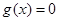 在
在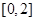 上有2个相等实根,即函数
上有2个相等实根,即函数 在
在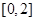 上有一个零点。
上有一个零点。
则 ,得
,得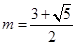 ……………………………………10分
……………………………………10分
②若 有2个零点,1个在
有2个零点,1个在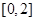 内,另1个在
内,另1个在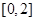 外,
外,
则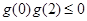 ,即
,即 ,解得
,解得 ,或
,或 …………12分
…………12分
经检验 有2个零点,不满足题意。
有2个零点,不满足题意。
综上: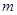 的取值范围是
的取值范围是 ,或
,或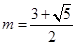 ,或
,或 ……………………14分
……………………14分
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com