
【题目】已知函数![]() 且在
且在![]() 上的最大值为
上的最大值为![]() ,
,
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,π)内的零点个数,并加以证明
【答案】(1)![]() (2)2个零点.
(2)2个零点.
【解析】
(1)由题意,可借助导数研究函数![]() 上的单调性,确定出最值,令最值等于
上的单调性,确定出最值,令最值等于![]() ,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解;(2)借助导数研究函数f(x)在(0,π)内单调性,由零点判定定理即可得出零点的个数.
,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解;(2)借助导数研究函数f(x)在(0,π)内单调性,由零点判定定理即可得出零点的个数.
(1)由已知得f′(x)=a(sinx+xcosx),对于任意的x∈(0, ![]() ),
),
有sinx+xcosx>0,当a=0时,f(x)= ![]() ,不合题意;
,不合题意;
当a<0时,x∈(0,![]() ),f′(x)<0,从而f(x)在(0,
),f′(x)<0,从而f(x)在(0, ![]() )单调递减,
)单调递减,
又函数f(x)=axsinx![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上图象是连续不断的,
]上图象是连续不断的,
故函数在[0, ![]() ]上的最大值为f(0),不合题意;
]上的最大值为f(0),不合题意;
当a>0时,x∈(0, ![]() ),f′(x)>0,从而f(x)在(0,
),f′(x)>0,从而f(x)在(0, ![]() )单调递增,
)单调递增,
又函数f(x)=axsinx ![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上图象是连续不断的,
]上图象是连续不断的,
故函数在[0, ![]() ]上上的最大值为f(
]上上的最大值为f(![]() )=
)=![]() a
a![]() =
=![]() ,解得a=1,
,解得a=1,
综上所述,得![]() ;
;
(2)函数f(
由(I)知,f(x)=xsinx![]() ,从而有f(0)=
,从而有f(0)= ![]() <0,f(
<0,f(![]() )=π32>0,
)=π32>0,
又函数在[0, ![]() ]上图象是连续不断的,所以函数f(x)在(0,
]上图象是连续不断的,所以函数f(x)在(0, ![]() )内至少存在一个零点,
)内至少存在一个零点,
又由(I)知f(x)在(0, ![]() )单调递增,故函数f(x)在(0,
)单调递增,故函数f(x)在(0, ![]() )内仅有一个零点。
)内仅有一个零点。
当x∈[![]() ,π]时,令g(x)=f′(x)=sinx+xcosx,
,π]时,令g(x)=f′(x)=sinx+xcosx,
由g(![]() )=1>0,g(π)=π<0,且g(x)在[
)=1>0,g(π)=π<0,且g(x)在[![]() ,π]上的图象是连续不断的,
,π]上的图象是连续不断的,
故存在m∈![]() ,π),使得g(m)=0.
,π),使得g(m)=0.
由g′(x)=2cosxxsinx,知x∈(![]() ,π)时,有g′(x)<0,
,π)时,有g′(x)<0,
从而g(x)在[![]() ,π]上单调递减。
,π]上单调递减。
当x∈![]() ,m),g(x)>g(m)=0,即f′(x)>0,
,m),g(x)>g(m)=0,即f′(x)>0,
从而f(x)在(![]() ,m)内单调递增
,m)内单调递增
故当x∈(![]() ,m)时,f(x)>f(π2)=π32>0,
,m)时,f(x)>f(π2)=π32>0,
从而(x)在(![]() ,m)内无零点;
,m)内无零点;
当x∈(m,π)时,有g(x)<g(m)=0,即f′(x)<0,
从而f(x)在(![]() ,m)内单调递减。
,m)内单调递减。
又f(m)>0,f(π)<0且f(x)在[m,π]上的图象是连续不断的,
从而f(x)在[m,π]内有且仅有一个零点。
综上所述,函数f(x)在(0,π)内有且仅有两个零点。


科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
(1)求圆![]() 的普通方程及其极坐标方程;
的普通方程及其极坐标方程;
(2)设直线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() (异于极点),与直线
(异于极点),与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公比大于
是公比大于![]() 的等比数列,
的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.数列
成等差数列.数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 满足
满足![]() ,且
,且![]() ,
,
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令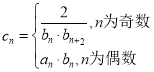 ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() ;
;
(3)将数列![]() ,
,![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个长为![]() ,宽为
,宽为![]() 的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
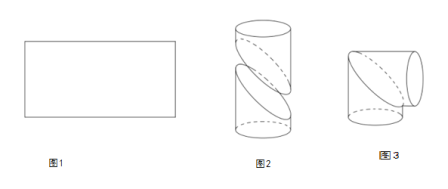
(1)求直角圆形弯管(图3)的体积;
(2)求斜截面椭圆的焦距;
(3)在相应的图1中建立适当的坐标系,使所画的曲线的方程为![]() ,求出方程并画出大致图像;
,求出方程并画出大致图像;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于
(t为参数),直线l与曲线C分别交于![]() 两点.
两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪,直到1872年,德国数学家戴德金提出了“戴德金分割”,才结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中不可能成立的是
,下列选项中不可能成立的是
A.![]() 没有最大元素,
没有最大元素,![]() 有一个最小元素
有一个最小元素
B.![]() 没有最大元素,
没有最大元素,![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素,![]() 有一个最小元素
有一个最小元素
D.![]() 有一个最大元素,
有一个最大元素,![]() 没有最小元素
没有最小元素
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com